
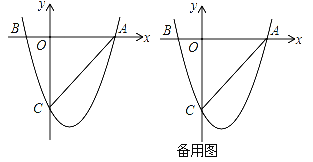
【題目】如圖,二次函數(shù)y=ax2+bx+c(a≠0)的圖象與x軸交于A(3,0),B(﹣1,0)兩點,與y軸相交于點C(0,﹣3)
(1)求該二次函數(shù)的解析式;
(2)設(shè)E是y軸右側(cè)拋物線上異于點A的一個動點,過點E作x軸的平行線交拋物線于另一點F,過點F作FG垂直于x軸于點G,再過點E作EH垂直于x軸于點H,得到矩形EFGH,則在點E的運動過程中,當(dāng)矩形EFGH為正方形時,求出該正方形的邊長;
(3)設(shè)P點是x軸下方的拋物線上的一個動點,連接PA、PC,求△PAC面積的取值范圍,若△PAC面積為整數(shù)時,這樣的△PAC有幾個?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,有5個.
,有5個.
【解析】試題分析:(1)設(shè)交點式為y=a(x+1)(x-3),然后把C點坐標(biāo)代入求出a即可;
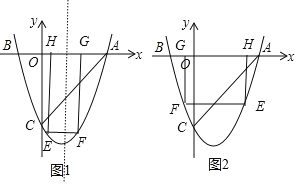
(2)設(shè)E(t,t2-2t-3),討論:當(dāng)0<t<1時,如圖1,EF=2(1-t),EH=-(t2-2t-3),利用正方形的性質(zhì)得2(1-t)=-(t2-2t-3);當(dāng)1<t<3時,如圖2,利用正方形的性質(zhì)得2(t-1)=-(t2-2t-3),當(dāng)t>3時,2(t-1)=t2-2t-3,然后分別解方程得到滿足條件的t的值,再計算出對應(yīng)的正方形的邊長;
(3)設(shè)P(x,x2-2x-3),討論:當(dāng)-1<x<0時,由于S△ABC=6,則0<S△APC<6,當(dāng)0<x<3時,作PM∥y軸交AC于點M,如圖3,求出直線AC的解析式為y=x-3,則M(x,x-3),利用三角形面積公式得S△APC=![]() 3(-x2+3x),利用二次函數(shù)的性質(zhì)得0<S△APC<
3(-x2+3x),利用二次函數(shù)的性質(zhì)得0<S△APC<![]() ,所以0<S△APC<6,于是得到△PAC面積為整數(shù)時,它的值為1、2、3、4、5.
,所以0<S△APC<6,于是得到△PAC面積為整數(shù)時,它的值為1、2、3、4、5.
試題解析:(1)設(shè)拋物線解析式為y=a(x+1)(x3),
把C(0,3)代入得3a=3,解得a=1,
所以拋物線解析式為y=(x+1)(x3),
即y=x22x3;
(2)拋物線的對稱軸為直線x=1,
設(shè)E(t,t22t3),
當(dāng)0<t<1時,如圖1,EF=2(1t),EH=(t22t3),
∵矩形EFGH為正方形,
∴EF=EH,即2(1t)=(t22t3),
整理得t24t1=0,解得t1=2+![]() (舍去),t2=2
(舍去),t2=2![]() (舍去);
(舍去);
當(dāng)1<t<3時,如圖2,EF=2(t1),EH=(t22t3),
∵矩形EFGH為正方形,
∴EF=EH,即2(t1)=(t22t3),
整理得t25=0,解得t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
此時正方形EFGH的邊長為2![]() 2;
2;
當(dāng)t>3時,EF=2(t1),EH=t22t3,
∵矩形EFGH為正方形,
∴EF=EH,即2(t1)=t22t3,
整理得t24t1=0,解得t1=2+![]() ,t2=2
,t2=2![]() (舍去),
(舍去),
此時正方形EFGH的邊長為2![]() +2,
+2,
綜上所述,正方形EFGH的邊長為2![]() 2或2
2或2![]() +2;
+2;
(3)設(shè)P(x,x22x3),
當(dāng)1<x<0時,
∵S△ABC=![]() ×4×3=6,
×4×3=6,
∴0<S△APC<6,
當(dāng)0<x<3時,作PM∥y軸交AC于點M,如圖3,
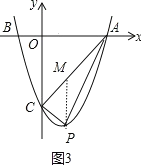
易得直線AC的解析式為y=x3,則M(x,x3),
∴PM=x3(x22x3)=x2+3x,
∴S△APC=![]() ×3(x2+3x)=
×3(x2+3x)=![]() x2+
x2+![]() x=
x=![]() (x
(x![]() )2+
)2+![]() ,
,
當(dāng)x=![]() 時,S△APC的面積的最大值為
時,S△APC的面積的最大值為![]() ,即0<S△APC<
,即0<S△APC<![]() ,
,
綜上所述,0<S△APC<6,
∴△PAC面積為整數(shù)時,它的值為1、2、3、4、5,即△PAC有5個.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】探究規(guī)律:我們有可以直接應(yīng)用的結(jié)論:若兩條直線平行,那么在一條直線上任取一點,無論這點在直線的什么位置,這點到另一條直線的距離均相等.例如:如圖1,兩直線![]() ∥
∥![]() ,兩點
,兩點![]() ,
,![]() 在
在![]() 上,
上,![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,則
,則![]() .
.
如圖2,已知直線![]() ∥
∥![]() ,
,![]() ,
,![]() 為直線
為直線![]() 上的兩點,
上的兩點,![]() .
.![]() 為直線
為直線![]() 上的兩點.
上的兩點.
(1)請寫出圖中面積相等的各對三角形: .
(2)如果![]() ,
,![]() ,
,![]() 為三個定點,點
為三個定點,點![]() 在
在![]() 上移動,那么無論
上移動,那么無論![]() 點移動到任何位置,總有: 與
點移動到任何位置,總有: 與![]() 的面積相等;理由是: .
的面積相等;理由是: .

解決問題:
如圖3,五邊形![]() 是張大爺十年前承包的一塊土地的示意圖,經(jīng)過多年開墾荒地,現(xiàn)已變成如圖4所示的形狀,但承包土地與開墾荒地的分界小路(圖4中折線
是張大爺十年前承包的一塊土地的示意圖,經(jīng)過多年開墾荒地,現(xiàn)已變成如圖4所示的形狀,但承包土地與開墾荒地的分界小路(圖4中折線![]() )還保留著,張大爺想過點
)還保留著,張大爺想過點![]() 修一條直路,直路修好后,要保持直路左邊的土地面積與承包時的一樣多.請你用以上的幾何知識,按張大爺?shù)囊笤O(shè)計出修路方案.(不計分界小路與直路的占地面積)
修一條直路,直路修好后,要保持直路左邊的土地面積與承包時的一樣多.請你用以上的幾何知識,按張大爺?shù)囊笤O(shè)計出修路方案.(不計分界小路與直路的占地面積)
(1)寫出設(shè)計方案,并在圖4中畫出相應(yīng)的圖形;
(2)說明方案設(shè)計理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
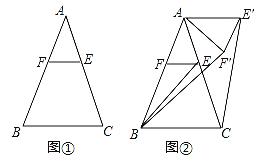
【題目】已知,△ABC中,AB=AC,點E是邊AC上一點,過點E作EF∥BC交AB于點F
(1)如圖①,求證:AE=AF;
(2)如圖②,將△AEF繞點A逆時針旋轉(zhuǎn)α(0°<α<144°)得到△AE′F′.連接CE′BF′.
①若BF′=6,求CE′的長;
②若∠EBC=∠BAC=36°,在圖②的旋轉(zhuǎn)過程中,當(dāng)CE′∥AB時,直接寫出旋轉(zhuǎn)角α的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】新能源汽車環(huán)保節(jié)能,越來越受到消費者的喜愛.各種品牌相繼投放市場.一汽貿(mào)公司經(jīng)銷某品牌新能源汽車.去年銷售總額為5000萬元,今年1~5月份,每輛車的銷售價格比去年降低1萬元.銷售數(shù)量與去年一整年的相同.銷售總額比去年一整年的少20%,今年1~5月份每輛車的銷售價格是多少萬元?設(shè)今年1~5月份每輛車的銷售價格為x萬元.根據(jù)題意,列方程正確的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
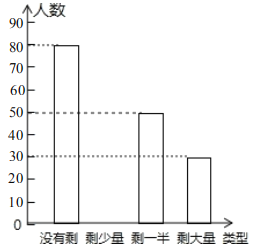
【題目】為更好地踐行社會主義核心價值觀,讓同學(xué)們珍惜糧食,學(xué)會感恩,校學(xué)生會積極倡導(dǎo)“光盤小行動”,某天午餐后學(xué)生會干部隨機調(diào)查了部分同學(xué)就餐飯菜的剩余情況,并將結(jié)果統(tǒng)計后繪制成了如圖所示的不完整的統(tǒng)計圖.
(1)這次被調(diào)查的同學(xué)共有 名;
(2)補全條形統(tǒng)計圖;
(3)計算在扇形統(tǒng)計圖中剩大量飯菜所對應(yīng)扇形圓心的度數(shù);
(4)校學(xué)生會通過數(shù)據(jù)分析,估計這次被調(diào)查的所有學(xué)生一餐浪費的食物可以供50人用一餐,據(jù)此估算,全校![]() 名學(xué)生一餐浪費的食物可供多少人食用一餐?
名學(xué)生一餐浪費的食物可供多少人食用一餐?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
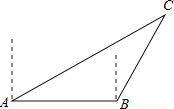
【題目】海中有一燈塔C,它的周圍12海里有暗礁,漁船跟蹤魚群由西向東航行![]() 在A處測得燈塔C在北偏東60°,航行20海里后到達B點,這時測得燈塔C在北偏東30°,如果漁船不改變航向,繼續(xù)向東航行,有沒有觸礁的危險?
在A處測得燈塔C在北偏東60°,航行20海里后到達B點,這時測得燈塔C在北偏東30°,如果漁船不改變航向,繼續(xù)向東航行,有沒有觸礁的危險?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】貴州省是我國首個大數(shù)據(jù)綜合試驗區(qū),大數(shù)據(jù)在推動經(jīng)濟發(fā)展、改善公共服務(wù)等方面日益顯示出巨大的價值,為創(chuàng)建大數(shù)據(jù)應(yīng)用示范城市,我市某機構(gòu)針對市民最關(guān)心的四類生活信息進行了民意調(diào)查(被調(diào)查者每人限選一項),下面是部分四類生活信息關(guān)注度統(tǒng)計圖表,請根據(jù)圖中提供的信息解答下列問題:

(1)本次參與調(diào)查的人數(shù)有 人;
(2)關(guān)注城市醫(yī)療信息的有 人,并補全條形統(tǒng)計圖;
(3)扇形統(tǒng)計圖中,D部分的圓心角是 度;
(4)說一條你從統(tǒng)計圖中獲取的信息.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一架梯子的長度為25米,斜靠在墻上,梯子低部離墻底端為7米.
(1)這個梯子頂端離地面有 米;
(2)如果梯子的頂端下滑了4米,那么梯子的底部在水平方向滑動了幾米?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有規(guī)律排列的一列數(shù):2,4,6,8,10,12,…,它的每一項可用式子2n(n是正整數(shù))來表示.那么有規(guī)律排列的一列數(shù):-1,2,-4,7,-11,16,-22,29,….
(1)它的第10個數(shù)是多少?
(2)你認為它的第n項可用怎樣的式子來表示?
(3)2018是不是這列數(shù)中的數(shù)?如果是,是第幾個數(shù)?如果不是,請說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com