
【題目】探究規律:我們有可以直接應用的結論:若兩條直線平行,那么在一條直線上任取一點,無論這點在直線的什么位置,這點到另一條直線的距離均相等.例如:如圖1,兩直線![]() ∥
∥![]() ,兩點
,兩點![]() ,
,![]() 在
在![]() 上,
上,![]() ⊥
⊥![]() 于
于![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,則
,則![]() .
.
如圖2,已知直線![]() ∥
∥![]() ,
,![]() ,
,![]() 為直線
為直線![]() 上的兩點,
上的兩點,![]() .
.![]() 為直線
為直線![]() 上的兩點.
上的兩點.
(1)請寫出圖中面積相等的各對三角形: .
(2)如果![]() ,
,![]() ,
,![]() 為三個定點,點
為三個定點,點![]() 在
在![]() 上移動,那么無論
上移動,那么無論![]() 點移動到任何位置,總有: 與
點移動到任何位置,總有: 與![]() 的面積相等;理由是: .
的面積相等;理由是: .

解決問題:
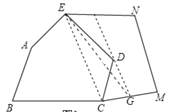
如圖3,五邊形![]() 是張大爺十年前承包的一塊土地的示意圖,經過多年開墾荒地,現已變成如圖4所示的形狀,但承包土地與開墾荒地的分界小路(圖4中折線
是張大爺十年前承包的一塊土地的示意圖,經過多年開墾荒地,現已變成如圖4所示的形狀,但承包土地與開墾荒地的分界小路(圖4中折線![]() )還保留著,張大爺想過點
)還保留著,張大爺想過點![]() 修一條直路,直路修好后,要保持直路左邊的土地面積與承包時的一樣多.請你用以上的幾何知識,按張大爺的要求設計出修路方案.(不計分界小路與直路的占地面積)
修一條直路,直路修好后,要保持直路左邊的土地面積與承包時的一樣多.請你用以上的幾何知識,按張大爺的要求設計出修路方案.(不計分界小路與直路的占地面積)
(1)寫出設計方案,并在圖4中畫出相應的圖形;
(2)說明方案設計理由.
【答案】探究規律:(1)![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() ;(2)
;(2)![]() ; 同底等高的兩個三角形的面積相等;解決問題:(1)方案見解析;(2)理由見解析.
; 同底等高的兩個三角形的面積相等;解決問題:(1)方案見解析;(2)理由見解析.
【解析】分析:(1)根據同底等高的三角形的面積相等與三角形的面積的和差關系求解;(2)①結合三角形的面積公式回答;②根據平行線間的距離處處相等和同底等高的兩三角形面積相等設計方案.
詳解:(1)![]() 和
和![]() ,
,![]() 和
和![]() ,
,![]() 和
和![]() .
.
(2)![]() ;同底等高的兩個三角形的面積相等.
;同底等高的兩個三角形的面積相等.
連接![]() ,過
,過![]() 點作
點作![]() 的平行線
的平行線![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
![]() 就是所求的道路.
就是所求的道路.
設EF交CD于點H,
∵EC∥DF,
∴D和F點到EC的距離相等(平行線間的距離處處相等),
又∵EC=EC,
∴S△ECF=S△ECD(同底等高的兩三角形面積相等),
∴S五邊形ABCDE=S五邊形EDCMN,S五邊形EDCMN=S四邊形EFMN.
即:EF為直路的位置可以保持直路左邊的土地面積與承包時的一樣多,右邊的土地面積與開墾的荒地面積一樣多


科目:初中數學 來源: 題型:
【題目】一個自然數m,若將其數字重新排列可得一個新的自然數n,如果m=3n,我們稱m是一個“希望數”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)請說明41不是希望數,并證明任意兩位數都不可能是“希望數”.
(2)一個四位“希望數”M記為![]() ,已知
,已知![]() ,且c=2,請求出這個四位“希望數”.
,且c=2,請求出這個四位“希望數”.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=60°,作邊長為1的正六邊形A1B1C1D1E1F1 , 邊A1B1、F1E1分別在射線OM、ON上,邊C1D1所在的直線分別交OM、ON于點A2、F2 , 以A2F2為邊作正六邊形A2B2C2D2E2F2 , 邊C2D2所在的直線分別交OM、ON于點A3、F3 , 再以A3F3為邊作正六邊形A3B3C3D3E3F3 , …,依此規律,經第n次作圖后,點Bn到ON的距離是 . 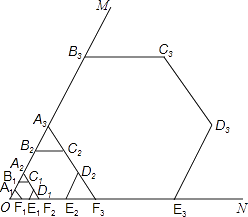
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年“五一”節,小明外出爬山,他從山腳爬到山頂的過程中,中途休息了一段時間.設他從山腳出發后所用的時間為t(分鐘),所走的路程為s(米),s與t之間的函數關系如圖所示,下列說法錯誤的是( )

A.小明中途休息用了20分鐘
B.小明休息前爬山的平均速度為每分鐘70米
C.小明在上述過程中所走的路程為6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是線段AB的中點,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求證:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲騎自行車、乙騎摩托車沿相同路線由A地到B地,行駛過程中路程與時間關系的圖像如圖所示.根據圖像解答下列問題:
(1)誰先出發?先出發多少時間?誰先到達終點?先到多少時間?
(2)分別求出甲、乙兩人的行駛速度;
(3)在什么時間段內,兩人均行駛在途中?(不包括起點和終點)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF翻折,點A恰好落在BC邊的A′處,若AB= ![]() ,∠EFA=60°,則四邊形A′B′EF的周長是( )
,∠EFA=60°,則四邊形A′B′EF的周長是( ) 
A.1+3 ![]()
B.3+ ![]()
C.4+ ![]()
D.5+ ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一只螞蟻在一個半圓形的花壇的周邊尋找食物,如圖1,螞蟻從圓心O出發,按圖中箭頭所示的方向,依次爬完下列三條線路:(1)線段OA、(2)半圓弧AB、(3)線段BO后,回到出發點。已知螞蟻在爬行過程中保持勻速,且在尋找到食物后停下來吃了2分鐘。螞蟻離出發點的距離s(螞蟻所在位置與O點之間線段的長度)與時間t之間的圖象如圖2所示,問:
(1)花壇的半徑是_______米,螞蟻是在上述三條線路中的哪條上尋找到了食物_________(填(1)、(2)、或(3));
(2)螞蟻的速度是_______米/分鐘;

(3)螞蟻從O點出發,直到回到O點,一共用時多少分鐘?(![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com