
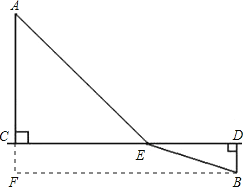
【題目】如圖,A,B兩個工廠位于一段直線形河的異側,A廠距離河邊AC=5km,B廠距離河邊BD=1km,經測量CD=8km,現準備在河邊某處(河寬不計)修一個污水處理廠E.
(1)設ED=x,請用x的代數式表示AE+BE的長;
(2)為了使兩廠的排污管道最短,污水廠E的位置應怎樣來確定此時需要管道多長?
(3)通過以上的解答,充分展開聯想,運用數形結合思想,請你猜想![]() 的最小值為多少?
的最小值為多少?

【答案】(1)AE+BE=![]() ;(2)此時最少需要管道10km;(3)最小值為13.
;(2)此時最少需要管道10km;(3)最小值為13.
【解析】
(1)由ED=x,AC⊥CD、BD⊥CD,根據勾股定理可用x表示出AE+BE的長;(2)根據兩點之間線段最短可知連接AB與CD的交點就是污水處理廠E的位置.過點B作BF⊥AC于F,構造出直角三角形,利用勾股定理求出AB的長即可;(3)根據AE+BE=![]() +
+![]() =AB=10;即可猜想所求代數式的值.
=AB=10;即可猜想所求代數式的值.
(1)在Rt△ACE和Rt△BDE中,根據勾股定理可得AE=![]() ,BE=
,BE=![]() ,
,
∴AE+BE=![]() +
+![]() ;
;
(2)根據兩點之間線段最短可知連接AB與CD的交點就是污水處理廠E的位置.
過點B作BF⊥AC于F,則有BF=CD=8,BD=CF=1.
∴AF=AC+CF=6.
在Rt△ABF中,BA=![]() =
=![]() =10,
=10,
∴此時最少需要管道10km.
(3)根據以上推理,設ED=x.AC=3,DB=2,CD=12.
∴當A、E、B共線時求出AB的值即為原式最小值.
當A、E、B共線時![]() +
+![]() =
=![]() =13,即其最小值為13.
=13,即其最小值為13.


科目:初中數學 來源: 題型:
【題目】已知:如圖,E、F是四邊形ABCD的對角線AC上的兩點,AF=CE,DF=BE,DF∥BE.

求證:(1)△AFD≌△CEB.(2)四邊形ABCD是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 三個城市在同一直線上(
三個城市在同一直線上(![]() 市在
市在![]() 兩市之間),甲、乙兩車分別從
兩市之間),甲、乙兩車分別從![]() 市、
市、![]() 市同時出發沿著直線公路相向而行,兩車均保持勻速行駛,已知甲車的速度大于乙車的速度,且當甲車到達
市同時出發沿著直線公路相向而行,兩車均保持勻速行駛,已知甲車的速度大于乙車的速度,且當甲車到達![]() 市時,甲、乙兩車都停止運動,甲、乙兩車到
市時,甲、乙兩車都停止運動,甲、乙兩車到![]() 市的距離之和
市的距離之和![]() (千米)與甲車行駛的時間
(千米)與甲車行駛的時間![]() (小時)之間的關系如圖所示,則當乙車到達
(小時)之間的關系如圖所示,則當乙車到達![]() 市時,甲車離
市時,甲車離![]() 市還有_______千米.
市還有_______千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市規定了每月用水18立方米以內(含18立方米)和用水18立方米以上兩種不同的收費標準.該市的用戶每月應交水費y(元)是用水量x(立方米)的函數,其圖象如圖所示.

(1)若某月用水量為18立方米,則應交水費多少元?
(2)當用水18立方米以上時,每立方米應交水費多少元?
(3)若小敏家某月交水費81元,則這個月用水量為多少立方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1,圖2是兩張形狀和大小完全相同的方格紙,方格紙中每個小正方形的邊長均為1,線段AB的兩個端點均在小正方形的頂點上.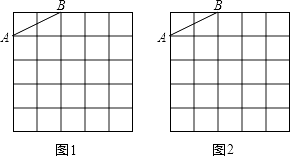
(1)如圖1,在小正方形的頂點上確定一點C,連接AC、BC,使得△ABC為直角三角形,其面積為5,并直接寫出△ABC的周長;
(2)如圖2,在小正方形的頂點上確定一點D,連接AD、BD,使得△ABD中有一個內角為45°,且面積為3.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用一根長是20 cm的細繩圍成一個長方形,這個長方形的一邊長為x cm,它的面積為y cm2.

(1)寫出y與x之間的關系式;
(2)用表格表示當x從1變到9時(每次增加1),y的相應值;
(3)從上面的表格中,你看出什么規律?(寫出一條即可)
(4)從表格中可以發現怎樣圍,得到的長方形的面積最大?最大是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,動點P在平面直角坐標系中按圖中箭頭所示方向運動,第1次從原點運動到點(1,1),第2次接著運動到點(2,0),第3次接著運動到點(3,2),…,按這樣的運動規律,經過第2017次運動后,動點P的坐標是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB為⊙O的直徑,BM為⊙O的切線,點C為射線BM上一點,連接AC交⊙O于點D,點E為BC上一點.連接AE交半圓于F.
(1)如圖1,若AE平分∠BAC,求證:∠DBF=∠CBF;
(2)如圖2,過點D作⊙O的切線交BM于N,若DN⊥BM,求證:△ABC為等腰直角三角形;
(3)在(2)的條件下,如圖3,延長BF交AC于G,點H為AB上一點,且BH=2BE,過點H作AE的垂線交AC于P,連接OG交DN于K,若AP=CG,EF=1,求GK的長.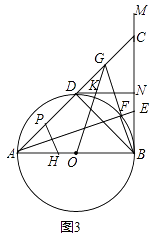
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知以Rt△ABC的邊AB為直徑作△ABC的外接圓⊙O,∠B的平分線BE交AC于D,交⊙O于E,過E作⊙O切線EF交BA的延長線于F.
(1)如圖1,求證:EF∥AC;
(2)如圖2,OP⊥AO交BE于點P,交FE的延長線于點M.求證:△PME是等腰三角形;
(3)如圖3,在(2)的條件下:CG⊥AB于H點,交⊙O于G點,交AC于Q點,如圖2,若sinF= ![]() ,EQ=5,求PM的值.
,EQ=5,求PM的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com