
【題目】完成題目:
(1)如圖1,已知△ABC,以AB、AC為邊向△ABC外作等邊△ABD和等邊△ACE,連接BE,CD,請你完成圖形,并證明:BE=CD;(尺規作圖,不寫作法,保留作圖痕跡);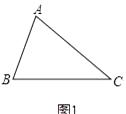
(2)如圖2,已知△ABC,以AB、AC為邊向外作正方形ABFD和正方形ACGE,連接BE,CD,BE與CD有什么數量關系?簡單說明理由;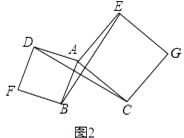
(3)運用(1)、(2)解答中所積累的經驗和知識,完成下題:
如圖3,要測量池塘兩岸相對的兩點B,E的距離,已經測得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的長.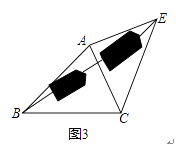
【答案】
(1)解:完成圖形,如圖所示:

證明:∵△ABD和△ACE都是等邊三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∵在△CAD和△EAB中,
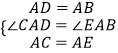 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD
(2)解:BE=CD,理由同(1),
∵四邊形ABFD和ACGE均為正方形,
∴AD=AB,AC=AE,∠BAD=∠CAE=90°,
∴∠CAD=∠EAB,
∵在△CAD和△EAB中,
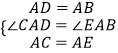 ,
,
∴△CAD≌△EAB(SAS),
∴BE=CD;
(3)解:由(1)、(2)的解題經驗可知,過A作等腰直角△ABD,∠BAD=90°,
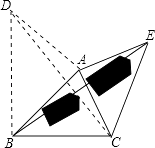
則AD=AB=100米,∠ABD=45°,
∴BD=100 ![]() 米,
米,
連接CD,BD,則由(2)可得BE=CD,
∵∠ABC=45°,∴∠DBC=90°,
在Rt△DBC中,BC=100米,BD=100 ![]() 米,
米,
根據勾股定理得:CD= ![]() =100
=100 ![]() 米,
米,
則BE=CD=100 ![]() 米.
米.
【解析】(1)分別以A、B為圓心,AB長為半徑畫弧,兩弧交于點D,連接AD,BD,同理連接AE,CE,如圖所示,由△ABD與△ACE都是等邊三角形,得到三對邊相等,兩個角相等,都為60度,利用等式的性質得到夾角相等,利用SAS得到△CAD與△EAB全等,利用全等三角形的對應邊相等即可得證;(2)BE=CD,理由與(1)同理;(3)根據(1)、(2)的經驗,過A作等腰直角△ABD,連接CD,由AB=AD=100,利用勾股定理求出BD的長,由題意得到△DBC為直角三角形,利用勾股定理求出CD的長,即為BE的長.


 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:初中數學 來源: 題型:
【題目】在一次體育達標測試中,九年級(2)班15名男生的引體向上成績如下表:問這15名男生的引體向上成績的中位數和眾數分別是( )
成績/個 | 8 | 9 | 11 | 12 | 13 | 15 |
人數 | 1 | 2 | 3 | 4 | 3 | 2 |
A.12,13B.12,12C.11,12D.3,4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某教育局為了解本地八年級學生參加社會實踐活動情況,隨機抽查了部分八年級學生第一學期參加社會實踐活動的天數,并用得到的數據繪制了兩幅統計圖,下面給出了兩幅不完整的統計圖(如圖) 
請根據圖中提供的信息,回答下列問題:
(1)α= , 并寫出該扇形所對圓心角的度數為 , 請補全條形圖 .
(2)在這次抽樣調查中,眾數和中位數分別是多少?
(3)如果該地共有八年級學生2000人,請你估計“活動時間不少于7天”的學生人數大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
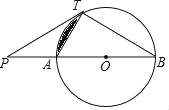
【題目】如圖,已知直線PT與⊙O相切于點T,直線PO與⊙O相交于A,B兩點.
(1)求證:PT2=PAPB;
(2)若PT=TB=![]() ,求圖中陰影部分的面積.
,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新農村社區改造中,有一部分樓盤要對外銷售,某樓盤共23層,銷售價格如下:第八層樓房售價為4000元/米2 , 從第八層起每上升一層,每平方米的售價提高50元;反之,樓層每下降一層,每平方米的售價降低30元,已知該樓盤每套樓房面積均為120米2 . 若購買者一次性付清所有房款,開發商有兩種優惠方案:
方案一:降價8%,另外每套樓房贈送a元裝修基金;
方案二:降價10%,沒有其他贈送.
(1)請寫出售價y(元/米2)與樓層x(1≤x≤23,x取整數)之間的函數關系式;
(2)老王要購買第十六層的一套樓房,若他一次性付清購房款,請幫他計算哪種優惠方案更加合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列多項式的乘法中,能使用平方差公式計算的有( )
①(m-n)(-m+n);②(-a-b)(a-b);③(x+y)(-x-y);④(x+3y-z)(x+z-3y)
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實行學案式教學,需印制若干份數學學案,印刷廠有甲、乙兩種收費方式,除按印數收取印刷費外,甲種方式還需收取制版費而乙種不需要.兩種印刷方式的費用y(元)與印刷份數x(份)之間的關系如圖所示: 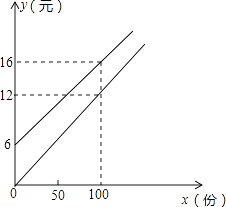
(1)填空:甲種收費的函數關系式是 . 乙種收費的函數關系式是 .
(2)該校某年級每次需印制100~450(含100和450)份學案,選擇哪種印刷方式較合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com