
【題目】如圖,在平面直角坐標系中,拋物線y=-![]() x2+
x2+![]() x+3與x軸交于A,B兩點(點A在點B左側),與y軸交于點C:連接BC,點P為線段BC上方拋物線上的一動點,連接OP交BC于點Q.
x+3與x軸交于A,B兩點(點A在點B左側),與y軸交于點C:連接BC,點P為線段BC上方拋物線上的一動點,連接OP交BC于點Q.
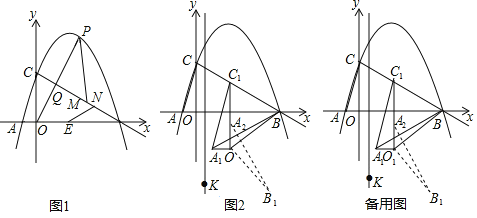
(1)如圖1,當![]() 值最大時,點E為線段AB上一點,在線段BC上有兩動點M,N(M在N上方),且MN=1,求PM+MN+NE-
值最大時,點E為線段AB上一點,在線段BC上有兩動點M,N(M在N上方),且MN=1,求PM+MN+NE-![]() BE的最小值;
BE的最小值;
(2)如圖2,連接AC,將△AOC沿射線CB方向平移,點A,C,O平移后的對應點分別記作A1,C1,O1,當C1B=O1B時,連接A1B、O1B,將△A1O1B繞點O1沿順時針方向旋轉90°后得△A2O1B1在直線x=![]() 上是否存在點K,使得△A2B1K為等腰三角形?若存在,直接寫出點K的坐標;不存在,請說明理由.
上是否存在點K,使得△A2B1K為等腰三角形?若存在,直接寫出點K的坐標;不存在,請說明理由.
【答案】(1)![]() ;(2)K1(
;(2)K1(![]() ,
,![]() ),K2(
),K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),K4(
,-5),K4(![]() ,
,![]() )
)
【解析】
(1)先求出拋物線與坐標軸的交點坐標,待定系數法求出直線BC解析式,過P作PT∥y軸交BC于T,構造△PTQ∽△ACQ,設點P的橫坐標為m,通過相似三角形性質得出![]() 關于m的函數表達式,利用二次函數最值即可;
關于m的函數表達式,利用二次函數最值即可;
(2)存在.先求出△AOC沿射線CB方向平移,并能使C1B=O1B時△A1O1B各頂點的坐標,在求出△A1O1B繞點O1沿順時針方向旋轉90°后得△A2O1B1的各頂點坐標,最后按照△A2B1K為等腰三角形進行分類討論即可.
解:(1)在拋物線y=-![]() x2+
x2+![]() x+3中,令x=0,得y=3,∴C(0,3);
x+3中,令x=0,得y=3,∴C(0,3);
令y=0,得-![]() x2+
x2+![]() x+3=0,解得:x1=-1,x2=4,∴B(4,0)
x+3=0,解得:x1=-1,x2=4,∴B(4,0)
設直線BC解析式為y=kx+b,將B(4,0),C(0,3);代入并解得:k=![]() ,b=3
,b=3
∴直線BC解析式為y=![]() x+3;
x+3;
過P作PT∥y軸交BC于T,設P(t,![]() +
+![]() +3),則T(t,
+3),則T(t,![]() +3),如圖所示:
+3),如圖所示:

∴PT=(![]() +
+![]() +3)-(
+3)-(![]() +3)=
+3)=![]() +3t,OC=3;
+3t,OC=3;
∵PT∥y軸
∴△PTQ∽△ACQ
∴![]() =
=![]() =
=![]() +t=
+t=![]()
∴當t=2時,![]() 值最大;此時,P(2,
值最大;此時,P(2,![]() ),PT=3;
),PT=3;
在Rt△BOC中,BC=![]() =5,
=5,
∴當NE⊥BC時,NE=![]() BE,此時,NE-
BE,此時,NE-![]() BE=0最小,
BE=0最小,
∵MN=1,∴PM+MN的最小值即PM最小值
∴PM⊥BC時,PM最小
過P作PM⊥BC于M,∴∠PMT=∠BOC=90°
∵∠PTM=∠BCO
∴![]() =
=![]()
∴PM=![]() PT=
PT=![]() ,
,
故PM+MN+NE-![]() BE的最小值=
BE的最小值=![]() ;
;
(2)存在.在△AOC中,∠AOC=90°,OA=1,OC=3,∴AC=![]()
如圖2,

由平移得:C1O1=OC=3,A1O1=OA=1,A1C1=AC=![]() ,
,
∵C1B=O1B,C1O1⊥OB
∴C1G=![]() C1O1=
C1O1=![]()
∴BG=2,OG=2
∴C1(2,![]() ),O1(2,
),O1(2,![]() ),A1(1,
),A1(1,![]() );
);
∴C1B=O1B=![]() ,A1B=
,A1B=![]() =
=![]() ;
;
∵△A1O1B繞點O1沿順時針方向旋轉90°后得△A2O1B1,
∴A2O1=1,O1B1=![]() ,A2B1=
,A2B1=![]() ;
;
∴A2(2,![]() ),B1(
),B1(![]() ,
,![]() )
)
∵△A2B1K為等腰三角形,
∴A2K=B1K或A2B1=B1K或A2K=A2B1,
設K(![]() ,m)
,m)
①當A2K=B1K時,則:![]() +
+![]() =
=![]() +
+![]() ,解得:m=-
,解得:m=-![]() ,∴K1(
,∴K1(![]() ,
,![]() ),
),
②當A2B1=B1K時,則:![]() +
+![]() =
=![]() ,解得:m1=-2,m2=-5,∴K2(
,解得:m1=-2,m2=-5,∴K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),
,-5),
③當A2K=A2B1時,則:![]() +
+![]() =
=![]() ,解得:m1=
,解得:m1=![]() (舍),m2=
(舍),m2=![]() ,∴K4(
,∴K4(![]() ,
,![]() );
);
綜上所述,點K的坐標為:K1(![]() ,
,![]() ),K2(
),K2(![]() ,-2),K3(
,-2),K3(![]() ,-5),K4(
,-5),K4(![]() ,
,![]() ).
).


 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】某文具店用1200元購進了A、B兩種羽毛球拍.已知A種羽毛球拍進價為每副12元,B種羽毛球拍進價為每副10元.文教店在銷售時A種羽毛球拍售價為每副15元,B種羽毛球拍售價為每副12元,全部售完后共獲利270元.
(1)求這個文教店購進A、B兩種羽毛球拍各多少副?
(2)若該文教店以原進價再次購進A、B兩種羽毛球拍,且購進A種羽毛球拍的數量不變,而購進B種羽毛球拍的數量是第一次的2倍,B種羽毛球拍按原售價銷售,而A種羽毛球拍降價銷售.當兩種羽毛球拍銷售完畢時,要使再次購進的羽毛球拍獲利不少于340元,A種羽毛球拍最低售價每副應為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=-x2+bx+c的頂點為C,對稱軸為直線x=1,且經過點A(3,-1),與y軸交于點B.
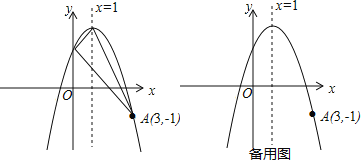
(1)求拋物線的解析式;
(2)判斷△ABC的形狀,并說明理由;
(3)經過點A的直線交拋物線于點P,交x軸于點Q,若S△OPA=2S△OQA,試求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() (
(![]() 為常數,且
為常數,且![]() )的圖象都經過點A(m,2).
)的圖象都經過點A(m,2).

(1)求點A的坐標及反比例函數的表達式;
(2)設一次函數![]() 的圖象與x軸交于點B,若點P是x軸上一點,且滿足△ABP的面積是2,直接寫出點P的坐標.
的圖象與x軸交于點B,若點P是x軸上一點,且滿足△ABP的面積是2,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初三有2000名學生,為了解初三學生的體能,從人數相等的甲、乙兩個班進行了抽樣調查,過程如下,請補充完整.
收集數據:從甲、乙兩個班各隨機抽取20名學生.進行了體能測試,測試成績(百分制)如下:
甲:78,86,74,81,75,76,87,70,75,90,75,79, 81,70, 74, 80 ,86, 69 ,83, 77.
乙:93,73,88,81,72,81,94,83,77,83,80,81,70,81,73,78,82,80,70,40.
整理、描述數據:按如下分數段整理、描述這兩組樣本數據:
成績 |
|
|
|
|
|
|
甲班 | 0 | 0 | 1 | 11 | 7 | 1 |
乙班 | 1 | 0 | 0 | 7 | 10 | 2 |
(說明:成績80分及以上為體能優秀,70~79分為體能良好,60~69分為體能合格,60分以下為體能不合格)
分析數據:兩組樣本數據的平均數、中位數、眾數如下表所示:
班級 | 平均數 | 中位數 | 眾數 | 優秀率 |
甲 | 78.3 | 77.5 | b | 40% |
乙 | 78 | a | 81 | c |
問題解決:
(1)表中a= ,b= ,c ;
(2)估計一下該校初三體能優秀的人數有多少人?
(3)通過以上數據的分析,你認為哪個班的學生的體能水平更高,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
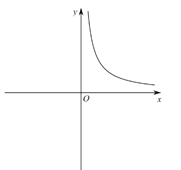
【題目】在研究反比例函數![]() 的圖象與性質時,我們對函數解析式進行了深入分析.
的圖象與性質時,我們對函數解析式進行了深入分析.
首先,確定自變量![]() 的取值范圍是全體非零實數,因此函數圖象會被
的取值范圍是全體非零實數,因此函數圖象會被![]() 軸分成兩部分;其次,分析解析式,得到
軸分成兩部分;其次,分析解析式,得到![]() 隨
隨![]() 的變化趨勢:當
的變化趨勢:當![]() 時,隨著
時,隨著![]() 值的增大,
值的增大,![]() 的值減小,且逐漸接近于零,隨著
的值減小,且逐漸接近于零,隨著![]() 值的減小,
值的減小,![]() 的值會越來越大…,由此,可以大致畫出
的值會越來越大…,由此,可以大致畫出![]() 在
在![]() 時的部分圖象,如圖所示:
時的部分圖象,如圖所示:
利用同樣的方法,我們可以研究函數![]() 的圖象與性質.通過分析解析式畫出部分函數圖象如圖所示.
的圖象與性質.通過分析解析式畫出部分函數圖象如圖所示.
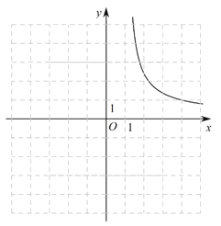
(1)請沿此思路在圖中完善函數圖象的草圖并標出此函數圖象上橫坐標為0的點![]() ;(畫出網格區域內的部分即可)
;(畫出網格區域內的部分即可)
(2)觀察圖象,寫出該函數的一條性質:__________;
(3)若關于![]() 的方程
的方程![]() 有兩個不相等的實數根,結合圖象,直接寫出實數
有兩個不相等的實數根,結合圖象,直接寫出實數![]() 的取值范圍: __________.
的取值范圍: __________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是中國古代數學專著,在數學上有其獨到的成就,不僅最早提到了分數問題,也首先記錄了“盈不足”等問題.如有一道闡述“盈不足”的問題,原文如下:今有共買雞,人出九,盈十一;人出六,不足十六.問人數、雞價各幾何?譯文為:現有若干人合伙出錢買雞,如果每人出9文錢,就會多11文錢;如果每人出6文錢,又會缺16文錢.問買雞的人數、雞的價格各是多少?請解答上述問題.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,與y軸交于點C對稱軸為直線x=1.直線y=﹣x+c與拋物線y=ax2+bx+c交于C、D兩點,D點在x軸下方且橫坐標小于3,則下列結論:
①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正確的有( )
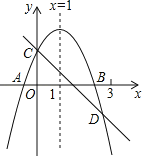
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com