
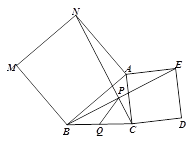
【題目】探究:如圖,分別以△ABC的兩邊AB和AC為邊向外作正方形ABMN和正方形ACDE,CN、BE交于點P. 求證:∠ANC = ∠ABE.
應用:Q是線段BC的中點,連結PQ. 若BC = 6,則PQ = ___________.
【答案】(1)證明見解析;(2)PQ=3
【解析】試題分析:根據正方形性質得出AN=AB,AC=AE,∠NAB=∠CAE=90°,求出∠NAC=∠BAE,證出△ANC≌△ABE即可.
試題解析:(1)∵四邊形ANMB和ACDE是正方形,
∴AN=AB,AC=AE,∠NAB=∠CAE=90°,
∵∠NAC=∠NAB+∠BAC,∠BAE=∠BAC+∠CAE,
∴∠NAC=∠BAE,
在△ANC和△ABE中
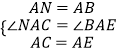
∴△ANC≌△ABE(SAS),
∴∠ANC=∠ABE.
(2)∵四邊形NABM是正方形,
∴∠NAB=90°,
∴∠ANC+∠AON=90°,
∵∠BOP=∠AON,∠ANC=∠ABE,
∴∠ABP+∠BOP=90°,
∴∠BPC=∠ABP+∠BOP=90°,
∵Q為BC中點,BC=6,
∴PQ=![]() BC=3,
BC=3,
故答案為:3.


科目:初中數學 來源: 題型:
【題目】某縣為了了解初中生對安全知識掌握情況,抽取了50名初中生進行安全知識測試,并將測試成績進行統計分析,繪制成了頻數分布表和頻數分布直方圖(未完成). 安全知識測試成績頻數分布表
組別 | 成績x(分數) | 組中值 | 頻數(人數) |
1 | 90≤x<100 | 95 | 10 |
2 | 80≤x<90 | 85 | 25 |
3 | 70≤x<80 | 75 | 12 |
4 | 60≤x<70 | 65 | 3 |

(1)完成頻數分布直方圖;
(2)這個樣本數據的中位數在第組;
(3)若將各組的組中值視為該組的平均成績,則此次測試的平均成績為;
(4)若將90分以上(含90分)定為“優秀”等級,則該縣10000名初中生中,獲“優秀”等級的學生約為人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初中學生帶手機上學,給學生帶來了方便,同時也帶來了一些負面影響.針對這種現象,某校九年級數學興趣小組的同學隨機調查了若干名家長對“初中學生帶手機上學”現象的看法,統計整理并制作了如圖的統計圖: 
(1)這次調查的家長總人數為人,表示“無所謂”的家長人數為人;
(2)隨機抽查一個接受調查的家長,恰好抽到“很贊同”的家長的概率是;
(3)求扇形統計圖中表示“不贊同”的扇形的圓心角度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,四根長度一定的木條,其中AB=6cm,CD=15cm,將這四根木條用小釘絞合在一起,構成一個四邊形ABCD(在A、B、C、D四點處是可以活動的).現固定AB邊不動,轉動這個四邊形,使它的形狀改變,在轉動的過程中有以下兩個特殊位置.
位置一:當點D在BA的延長線上時,點C在線段AD上(如圖2);
位置二:當點C在AB的延長線上時,∠C=90°.
(1)在圖2中,若設BC的長為![]() ,請用含
,請用含![]() 的代數式表示AD的長;
的代數式表示AD的長;
(2)在圖3中畫出位置二的示意圖
(3)利用圖2、圖3求圖1的四邊形ABCD中BC、AD邊的長度.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=2 ![]() ,∠C=120°,以點C為圓心的
,∠C=120°,以點C為圓心的 ![]() 與AB,AD分別相切于點G,H,與BC,CD分別相交于點E,F.若用扇形CEF作一個圓錐的側面,則這個圓錐的高是 .
與AB,AD分別相切于點G,H,與BC,CD分別相交于點E,F.若用扇形CEF作一個圓錐的側面,則這個圓錐的高是 . 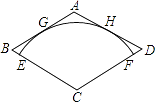
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于點D,PE⊥OB于點E.如果點M是OP的中點,則DM的長是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠ABC=45°,D是BC邊上的一點,BD=2,將△ACD沿直線AD翻折,點C剛好落在AB邊上的點E處.若P是直線AD上的動點,則△PEB的周長的最小值是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx﹣3a(a≠0)與x軸交于點A(﹣1,0)和點B,與y軸交于點C(0,2),連接BC.
(1)求該拋物線的解析式和對稱軸,并寫出線段BC的中點坐標;
(2)將線段BC先向左平移2個單位長度,再向下平移m個單位長度,使點C的對應點C1恰好落在該拋物線上,求此時點C1的坐標和m的值;
(3)若點P是該拋物線上的動點,點Q是該拋物線對稱軸上的動點,當以P,Q,B,C四點為頂點的四邊形是平行四邊形時,求此時點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年級(3)班數學興趣小組經過市場調查整理出某種商品在第x天(1≤x≤90,且x為整數)的售價與銷售量的相關信息如下.已知商品的進價為30元/件,設該商品的售價為y(單位:元/件),每天的銷售量為p(單位:件),每天的銷售利潤為w(單位:元).
時間x(天) | 1 | 30 | 60 | 90 |
每天銷售量p(件) | 198 | 140 | 80 | 20 |

(1)求出w與x的函數關系式;
(2)問銷售該商品第幾天時,當天的銷售利潤最大?并求出最大利潤;
(3)該商品在銷售過程中,共有多少天每天的銷售利潤不低于5600元?請直接寫出結果.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com