
【題目】如圖1,甲、乙兩車分別從相距480km的A、B兩地相向而行,乙車比甲車先出發1小時,并以各自的速度勻速行駛,甲車到達C地后因有事按原路原速返回A地.乙車從B地直達A地,兩車同時到達A地.甲、乙兩車距各自出發地的路程y(千米)與甲車出發所用的時間x(小時)的關系如圖2,結合圖象信息解答下列問題:
(1)乙車的速度是 千米/時,乙車行駛的時間t= 小時;
(2)求甲車從C地按原路原速返回A地的過程中,甲車距它出發地的路程y與它出發的時間x的函數關系式;
(3)直接寫出甲車出發多長時間兩車相距80千米.

【答案】(1) 乙車速度為:80千米/時,乙車行駛全程的時間6小時;(2)y=﹣120x+600;(3)甲車出發![]() 小時或3小時或
小時或3小時或![]() 兩車相距80千米
兩車相距80千米
【解析】
(1)結合題意,利用速度=路程÷時間,可得乙的速度、行駛時間;
(2)找到甲車到達C地和返回A地時x與y的對應值,利用待定系數法可求出函數解析式;
(3)甲、乙兩車相距80千米有兩種情況:
①相向而行:相等關系為“甲車行駛路程+乙車行駛路程+甲乙間距離=480”,
②同向而行:相等關系為“甲車距它出發地的路程+乙車路程﹣甲乙間距離=480”
分別根據相等關系列方程可求解.
解:(1)∵乙車比甲車先出發1小時,由圖象可知乙行駛了80千米,
∴乙車速度為:80千米/時,乙車行駛全程的時間t=480÷80=6(小時);
(2)根據題意可知甲從出發到返回A地需5小時,
∵甲車到達C地后因立即按原路原速返回A地,
∴結合函數圖象可知,當x=![]() 時,y=300;當x=5時,y=0;
時,y=300;當x=5時,y=0;
設甲車從C地按原路原速返回A地時,即![]() ≤x≤5,
≤x≤5,
甲車距它出發地的路程y與它出發的時間x的函數關系式為:y=kx+b,
將![]() 函數關系式得:
函數關系式得: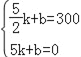 ,
,
解得:![]() ,
,
故甲車從C地按原路原速返回A地時,
甲車距它出發地的路程y與它出發的時間x的函數關系式為:y=﹣120x+600;
(3)由題意可知甲車的速度為:![]() =120(千米/時),
=120(千米/時),
設甲車出發m小時兩車相距80千米,有以下兩種情況:
①兩車相向行駛時,有:120m+80(m+1)+80=480,
解得:m=![]() ;
;
②兩車同向行駛時,有:600﹣120m+80(m+1)﹣80=480,
解得:m=3;
③兩車相遇之后,甲返回前,有120m+80(m+1)﹣80=480,
解得:m=![]() ;
;
∴甲車出發![]() 小時或3小時或
小時或3小時或![]() 兩車相距80千米.
兩車相距80千米.


科目:初中數學 來源: 題型:
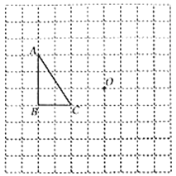
【題目】在如圖所示的正方形網格中,每個小正方形的邊長都是1個單位長度,![]() 的頂點均在格點上.(畫圖要求:先用
的頂點均在格點上.(畫圖要求:先用![]() 鉛筆畫圖,然后用黑色水筆描畫)
鉛筆畫圖,然后用黑色水筆描畫)
(1)①畫出![]() 繞點
繞點![]() 按逆時針方向旋轉
按逆時針方向旋轉![]() 后的
后的![]() ;
;
②連結![]() ,請判斷
,請判斷![]() 是怎樣的三角形,并簡要說明理由.
是怎樣的三角形,并簡要說明理由.
(2)畫出![]() ,使
,使![]() 和
和![]() 關于點
關于點![]() 成中心對稱;
成中心對稱;
(3)請指出如何平移![]() ,使得
,使得![]() 和
和![]() 能拼成一個長方形.
能拼成一個長方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將正方形紙片ABCD折疊,使點D落在邊AB上的D'處,點C落在C'處,若∠AD'M=50°,則∠MNC'的度數為( )

A. 100°B. 110°C. 120°D. 130°
查看答案和解析>>
科目:初中數學 來源: 題型:
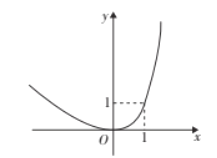
【題目】對于某一函數給出如下定義:若存在實數p,當其自變量的值為p時,其函數值等于p,則稱p為這個函數的不變值.在函數存在不變值時,該函數的最大不變值與最小不變值之差q稱為這個函數的不變長度.特別地,當函數只有一個不變值時,其不變長度q為零.例如:下圖中的函數有0,1兩個不變值,其不變長度q等于1.
(1)分別判斷函數y=x-1,y=x-1,y=x2有沒有不變值?如果有,直接寫出其不變長度;
(2)函數y=2x2-bx.
①若其不變長度為零,求b的值;
②若1≤b≤3,求其不變長度q的取值范圍;
(3) 記函數y=x2-2x(x≥m)的圖象為G1,將G1沿x=m翻折后得到的函數圖象記為G2,函數G的圖象由G1和G2兩部分組成,若其不變長度q滿足0≤q≤3,則m的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D、E分別是AB、AC的中點,過點E作EF∥AB,交BC于點F.
(1)求證:四邊形DBFE是平行四邊形;
(2)當△ABC滿足什么條件時,四邊形DBFE是菱形?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先填寫表,通過觀察后再回答問題:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | x | 1 | y | 100 | …… |
(1)表格中,x=_________,y=_________
(2)從表格中探究a與![]() 數位的規律,并利用這個規律解決下面兩個問題:
數位的規律,并利用這個規律解決下面兩個問題:
①已知![]() ,則
,則![]() ≈___________
≈___________
②已知![]() ,若
,若![]() ,用含m的代數式表示b,則b=___________
,用含m的代數式表示b,則b=___________
(3)試比較![]() 與a的大小(直接寫出結果)
與a的大小(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
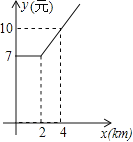
【題目】某地出租車計費方法如圖,x(km)表示行駛里程,y(元)表示車費,請根據圖象解答下列問題:
(1)該地出租車的起步價是 元;
(2)當x>2時,求y與x之間的函數關系式;
(3)若某乘客有一次乘出租車的里程為18km,則這位乘客需付出租車車費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
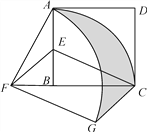
【題目】如圖,在正方形ABCD中,AD=2,E是AB的中點,將△BEC繞點B逆時針旋轉90°后,點E落在CB的延長線上點F處,點C落在點A處.再將線段AF繞點F順時針旋轉90°得線段FG,連結EF、CG.
(1)求證:EF∥CG;
(2)求點C、點A在旋轉過程中形成的![]() 、
、![]() 與線段CG所圍成的陰影部分的面積.
與線段CG所圍成的陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,∠B=∠C,AB=AC=12cm,BC=8cm,點D為AB的中點.如果點P在線段BC上以2cm/s的速度由B點向C點運動,同時,點Q在線段CA上由點C向A點運動.

(1)若點Q的運動速度與點P的運動速度相等,經過1秒后,△BPD與△CQP是否全等?請說明理由.
(2)若點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com