
【題目】二次函數(shù)![]() 的圖像過點(diǎn)
的圖像過點(diǎn)![]() ,且與
,且與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 在該拋物線的對稱軸上,若
在該拋物線的對稱軸上,若![]() 是以
是以![]() 為直角邊的直角三角形,則點(diǎn)
為直角邊的直角三角形,則點(diǎn)![]() 的坐標(biāo)為__________.
的坐標(biāo)為__________.
【答案】![]() 或
或![]()
【解析】
先求出點(diǎn)B的坐標(biāo)和拋物線的對稱軸,然后分兩種情況討論:當(dāng)∠ABM=90°時(shí),如圖1,過點(diǎn)M作MF⊥y軸于點(diǎn)F,易證△BFM∽△AOB,然后根據(jù)相似三角形的性質(zhì)可求得BF的長,進(jìn)而可得點(diǎn)M坐標(biāo);當(dāng)∠BAM=90°時(shí),輔助線的作法如圖2,同樣根據(jù)△BAE∽△AMH求出AH的長,繼而可得點(diǎn)M坐標(biāo).
解:對![]() ,當(dāng)x=0時(shí),y=3,∴點(diǎn)B坐標(biāo)為(0,3),
,當(dāng)x=0時(shí),y=3,∴點(diǎn)B坐標(biāo)為(0,3),
拋物線![]() 的對稱軸是直線:
的對稱軸是直線:![]() ,
,
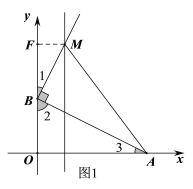
當(dāng)∠ABM=90°時(shí),如圖1,過點(diǎn)M作MF⊥y軸于點(diǎn)F,則![]() ,
,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
又∠MFB=∠BOA=90°,
∴△BFM∽△AOB,
∴![]() ,即
,即 ,解得:BF=3,
,解得:BF=3,
∴OF=6,
∴點(diǎn)M的坐標(biāo)是(![]() ,6);
,6);
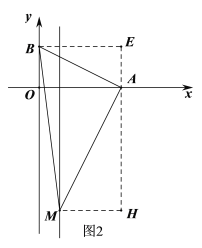
當(dāng)∠BAM=90°時(shí),如圖2,過點(diǎn)A作EH⊥x軸,過點(diǎn)M作MH⊥EH于點(diǎn)H,過點(diǎn)B作BE⊥EH于點(diǎn)E,則![]() ,
,
同上面的方法可得△BAE∽△AMH,
∴![]() ,即
,即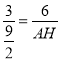 ,解得:AH=9,
,解得:AH=9,
∴點(diǎn)M的坐標(biāo)是(![]() ,﹣9);
,﹣9);
綜上,點(diǎn)M的坐標(biāo)是![]() 或
或![]() .
.
故答案為:![]() 或
或![]() .
.


 口算題天天練系列答案
口算題天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,過直線![]() 上一點(diǎn)
上一點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,線段
,線段![]() 交函數(shù)
交函數(shù)![]() 的圖像于點(diǎn)
的圖像于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 為線段
為線段![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 關(guān)于直線
關(guān)于直線![]() 的對稱點(diǎn)
的對稱點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
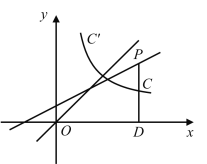
(1)求![]() 、
、![]() 的值;
的值;
(2)求直線![]() 與函數(shù)
與函數(shù)![]() 圖像的交點(diǎn)坐標(biāo);
圖像的交點(diǎn)坐標(biāo);
(3)直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】【提出問題】
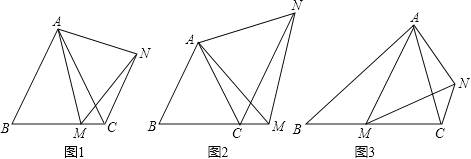
(1)如圖1,在等邊△ABC中,點(diǎn)M是BC上的任意一點(diǎn)(不含端點(diǎn)B、C),連結(jié)AM,以AM為邊作等邊△AMN,連結(jié)CN.求證:∠ABC=∠ACN.
【類比探究】
(2)如圖2,在等邊△ABC中,點(diǎn)M是BC延長線上的任意一點(diǎn)(不含端點(diǎn)C),其它條件不變,(1)中結(jié)論∠ABC=∠ACN還成立嗎?請說明理由.
【拓展延伸】
(3)如圖3,在等腰△ABC中,BA=BC,點(diǎn)M是BC上的任意一點(diǎn)(不含端點(diǎn)B、C),連結(jié)AM,以AM為邊作等腰△AMN,使頂角∠AMN=∠ABC.連結(jié)CN.試探究∠ABC與∠ACN的數(shù)量關(guān)系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知點(diǎn)A的坐標(biāo)為(0,2),點(diǎn)B的坐標(biāo)為(1,0),連結(jié)AB,以AB為邊在第一象限內(nèi)作正方形ABCD,直線BD交雙曲線y═![]() (k≠0)于D、E兩點(diǎn),連結(jié)CE,交x軸于點(diǎn)F.
(k≠0)于D、E兩點(diǎn),連結(jié)CE,交x軸于點(diǎn)F.

(1)求雙曲線y=![]() (k≠0)和直線DE的解析式.
(k≠0)和直線DE的解析式.
(2)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)C在以AB為直徑的![]() 上,點(diǎn)D是半圓AB的中點(diǎn),連接AC,BC,AD,BD,過點(diǎn)D作
上,點(diǎn)D是半圓AB的中點(diǎn),連接AC,BC,AD,BD,過點(diǎn)D作![]() 交CB的延長線于點(diǎn)H.
交CB的延長線于點(diǎn)H.
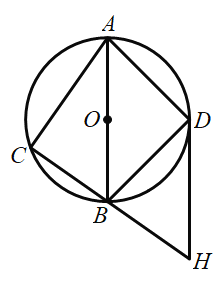
(1)求證:直線DH是![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求AD,BH的長.
,求AD,BH的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為邊
為邊![]() 上的一點(diǎn)(與
上的一點(diǎn)(與![]() 、
、![]() 不重合)四邊形
不重合)四邊形![]() 關(guān)于直線
關(guān)于直線![]() 的對稱圖形為四邊形
的對稱圖形為四邊形![]() ,延長
,延長![]() 交
交![]() 與點(diǎn)
與點(diǎn)![]() ,記四邊形
,記四邊形![]() 的面積為
的面積為![]() .
.
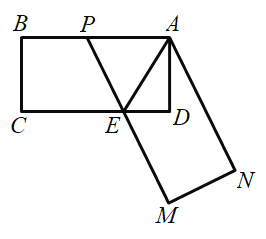
(1)若![]() ,求
,求![]() 的值;
的值;
(2)設(shè)![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式.
的函數(shù)表達(dá)式.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,某旅游景區(qū)為方便游客,修建了一條東西走向的木棧道 AB ,棧道 AB 與景區(qū)道路CD 平行.在 C 處測得棧道一端 A 位于北偏西 42°方向,在 D 處測得棧道另一端 B 位于北偏西 32°方向.已知 CD =120 m , BD =80 m ,求木棧道 AB 的長度(結(jié)果保留整數(shù)) .
(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了打好疫情期間的復(fù)工復(fù)產(chǎn)攻堅(jiān)戰(zhàn),某公司決定為員工采購一批口罩和消毒液,經(jīng)了解,購買4包口罩和3瓶消毒液共需要185元,購買8包口罩和5瓶消毒液共需要335元,
(1)一包口罩和一瓶消毒液各需要多少元?
(2)實(shí)際購買時(shí)發(fā)現(xiàn)廠家有兩種優(yōu)惠方案:方案一:購買口罩不超過20包時(shí),每包都按九折優(yōu)惠,超過20包時(shí),超過部分每包按七折優(yōu)惠;方案二:口罩和消毒液都按原價(jià)的八折優(yōu)惠,公司購買![]() 包口罩,10瓶消毒液.
包口罩,10瓶消毒液.
①求兩種方案下所需的費(fèi)用![]() (單位:元)與
(單位:元)與![]() (單位:包)的函數(shù)關(guān)系式;
(單位:包)的函數(shù)關(guān)系式;
②若該公司決定購買![]() 包口罩和10瓶消毒液,請你幫助該公司決定選擇哪種方案更合算.
包口罩和10瓶消毒液,請你幫助該公司決定選擇哪種方案更合算.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
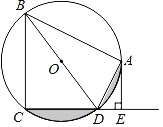
【題目】如圖,四邊形ABCD內(nèi)接于⊙O,BD是⊙O的直徑,AE⊥CD于點(diǎn)E,AD平分∠BDE.
(1)求證:AE是⊙O的切線;
(2)如果AB=6,AE=3,求:陰影部分面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com