
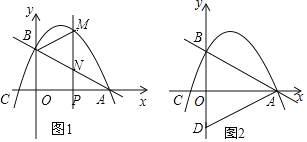
【題目】如圖1,拋物線![]() (
(![]() )與
)與![]() 軸交于點
軸交于點![]() 和點
和點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線解析式和![]() 點坐標;
點坐標;
(2)在![]() 軸上有一動點
軸上有一動點![]() ,過點
,過點![]() 作
作![]() 軸的垂線交直線
軸的垂線交直線![]() 于點
于點![]() ,交拋物線于點
,交拋物線于點![]() .當點
.當點![]() 位于第一象限圖象上,連接
位于第一象限圖象上,連接![]() ,求
,求![]() 面積的最大值及此時
面積的最大值及此時![]() 點的坐標;
點的坐標;
(3)如圖2,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,連接
,連接![]() .
.
①點![]() 是線段
是線段![]() 上一點(不與點
上一點(不與點![]() 重合),點
重合),點![]() 是線段
是線段![]() 上一點(不與點
上一點(不與點![]() 重合),則兩條線段之和
重合),則兩條線段之和![]() 的最小值為 ;
的最小值為 ;
②將![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() (
(![]() ),當點
),當點![]() 的對應點
的對應點![]() 落在
落在![]() 的邊所在直線上時,則此時點
的邊所在直線上時,則此時點![]() 的對應點
的對應點![]() 的坐標為 .
的坐標為 .
【答案】(1)![]() ,B(0,2);(2)4,M(2,3);(3)①
,B(0,2);(2)4,M(2,3);(3)①![]() ;②
;②![]() 或
或![]() 或
或![]()
【解析】
(1)將![]() 代入
代入![]() ,可求出
,可求出![]() 的值,將
的值,將![]() 的值代入即得到拋物線解析式,令
的值代入即得到拋物線解析式,令![]() ,求
,求![]() ,得點
,得點![]() 坐標;
坐標;
(2)待定系數法求出直線![]() 的解析式,設點
的解析式,設點![]() ,將
,將![]() 表示成
表示成![]() 的二次函數,配方成頂點式即可求得
的二次函數,配方成頂點式即可求得![]() 面積的最大值及此時
面積的最大值及此時![]() 點的坐標;
點的坐標;
(3)第①題求![]() 的最小值利用對稱進行轉化,應用“兩點之間線段最短”及“垂線段最短”可以得到“
的最小值利用對稱進行轉化,應用“兩點之間線段最短”及“垂線段最短”可以得到“![]() 的最小值”即為點
的最小值”即為點![]() 到直線
到直線![]() 的距離;第②題在
的距離;第②題在![]() 繞
繞![]() 逆時針旋轉過程中,按照依次落在直線
逆時針旋轉過程中,按照依次落在直線![]() 、
、![]() 、
、![]() 上分類討論.
上分類討論.
解:(1)將![]() 代入
代入![]() ,得
,得![]() ,
,
解得![]() ,
,
![]() 拋物線解析式為
拋物線解析式為![]() ,
,
令![]() ,得
,得![]() ,
,
![]() ;
;
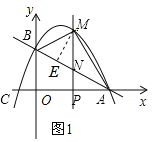
(2)如圖1,過點![]() 作
作![]() 于
于![]() ,設
,設![]() ,
,![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,將
,將![]() ,
,![]() 分別代入得
分別代入得![]() ,
,
解得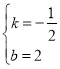 ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() ,
,![]() ,
,
![]() 當
當![]() 時,
時,![]() 的最大值
的最大值![]() ,
,
此時,點![]() 的坐標為
的坐標為![]() ;
;
(3)①如圖2,連接![]() 、
、![]() 、
、![]() ,則
,則![]() ,只有當
,只有當![]() 、
、![]() 、
、![]() 三點在同一直線上,且
三點在同一直線上,且![]() 時,
時,![]() 的值最小,
的值最小,
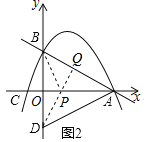
過點![]() 作
作![]() 于
于![]() ,交
,交![]() 軸于
軸于![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 、
、![]() 關于
關于![]() 軸對稱
軸對稱
![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() 的最小值
的最小值![]() ,
,
故答案為![]() .
.
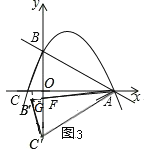
②如圖3,點![]() 落在直線
落在直線![]() 上,
上,
在拋物線![]() 中,令
中,令![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]()
由旋轉知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
設![]() 交
交![]() 軸于
軸于![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() ,
,
![]() ,
,![]()
![]() △
△![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,
![]()
![]()
![]()
![]()
![]() ,解得
,解得![]()
![]()
![]()
![]()
![]() △
△![]()
![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]()
![]() ;
;
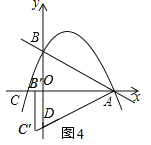
如圖4,點![]() 落在直線
落在直線![]() 上,
上,![]() ,
,
![]() 點
點![]() 的對應點
的對應點![]() 落在
落在![]() 軸上,由旋轉知:△
軸上,由旋轉知:△![]() ,
,
![]() ,
,![]()
![]()
![]() ;
;
如圖5,點![]() 落在直線
落在直線![]() 上,過
上,過![]() 作
作![]() 軸于
軸于![]() ,作
,作![]() 軸于
軸于![]() ,作
,作![]() 于
于![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在△ADQ和△![]() 中,
中,
 ,
,
∴△ADQ≌△![]() (AAS),
(AAS),
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
故答案為:![]() 或
或![]() 或
或![]() .
.



科目:初中數學 來源: 題型:
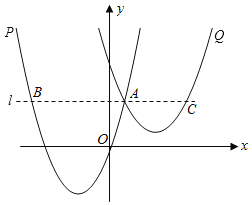
【題目】如圖,拋物線P:![]() 與拋物線Q:
與拋物線Q:![]() 在同一平面直角坐標系中(其中a,t均為常數,且t>0),已知點A(1,3)為拋物線P上一點,過點A作直線l∥x軸,與拋物線P交于另一點B.
在同一平面直角坐標系中(其中a,t均為常數,且t>0),已知點A(1,3)為拋物線P上一點,過點A作直線l∥x軸,與拋物線P交于另一點B.
(1)求a的值及點B的坐標;
(2)當拋物線Q經過點A時
①求拋物線Q的解析式;
②設直線l與拋物線Q的另一交點為C,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】事件發生的可能性有大有小,請你把下列事件發生可能性的大小按由小到大的順序排列起來__________.(只排序號)
①書包里有12本不同科目的教科書,隨手摸出一本,恰好是數學書;
②花2元買了一張彩票,就中了500萬大獎;
③我拋了兩次硬幣,都正面向上;
④若![]() ,則
,則![]() 和
和![]() 互為相反數.
互為相反數.
查看答案和解析>>
科目:初中數學 來源: 題型:
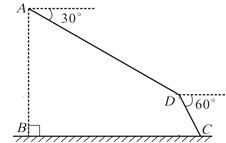
【題目】2017年9月8日—10日,第六屆翼裝飛行世界錦標賽在我市天門山風景區隆重舉行,來自全球11個國家的16名選手參加了激烈的角逐.如圖,某選手從離水平地面1000米高的A點出發(AB=1000米),沿俯角為![]() 的方向直線飛行1400米到達D點,然后打開降落傘沿俯角為
的方向直線飛行1400米到達D點,然后打開降落傘沿俯角為![]() 的方向降落到地面上的C點,求該選手飛行的水平距離
的方向降落到地面上的C點,求該選手飛行的水平距離![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“機動車行駛到斑馬線要禮讓行人”等交通法規實施后,某校數學課外實踐小組就對這些交通法規的了解情況在全校隨機調查了部分學生,調查結果分為四種:A.非常了解,B.比較了解,C.基本了解,D.不太了解,實踐小組把此次調查結果整理并繪制成下面不完整的條形統計圖和扇形統計圖.
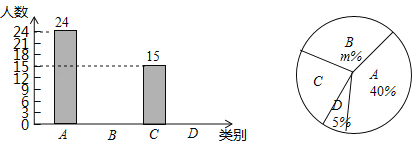
請結合圖中所給信息解答下列問題:
(1)填空:本次共調查_____名學生;扇形統計圖中C所對應扇形的圓心角度數是_____°;
(2)請直接補全條形統計圖;
(3)填空:扇形統計圖中,m的值為_____;
(4)該校共有500名學生,根據以上信息,請你估計全校學生中對這些交通法規“非常了解”的約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ABC=90°,∠BAC=30°,將△ABC繞點A順時針旋轉一定的角度![]() 得到△AED,點B、C的對應點分別是E、D.
得到△AED,點B、C的對應點分別是E、D.
(1)如圖1,當點E恰好在AC上時,求∠CDE的度數;
(2)如圖2,若![]() =60°時,點F是邊AC中點,求證:四邊形BFDE是平行四邊形.
=60°時,點F是邊AC中點,求證:四邊形BFDE是平行四邊形.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知O為圓錐的頂點,M為圓錐底面上一點,點P在OM上.一只蝸牛從P點出發,繞圓錐側面爬行,回到P點時所爬過的最短路線的痕跡如圖所示.若沿OM將圓錐側面剪開并展開,所得側面展開圖是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家發改委、工業和信息化部、財政部公布了“節能產品惠民工程”,公交公司積極響應將舊車換成節能環保公交車,計劃購買A型和B型兩種環保型公交車10輛,其中每臺的價格、年載客量如表:
A型 | B型 | |
價格(萬元/臺) | x | y |
年載客量/萬人次 | 60 | 100 |
若購買A型環保公交車1輛,B型環保公交車2輛,共需400萬元;若購買A型環保公交車2輛,B型環保公交車1輛,共需350萬元.
(1)求x、y的值;
(2)如果該公司購買A型和B型公交車的總費用不超過1200萬元,且確保10輛公交車在該線路的年載客量總和不少于680萬人次,問有哪幾種購買方案?
(3)在(2)的條件下,哪種方案使得購車總費用最少?最少費用是多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場為方便消費者購物,準備將原來的階梯式自動扶梯改造成斜坡式自動扶梯,如圖,已知原階梯式自動扶梯AB的長為6![]() m,坡角∠ABE=45°,改造后的斜坡自動扶梯坡角∠ACB=15°,求改造后的斜坡式自動扶梯AC的長,(精確到0.1m,參考數據;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27)
m,坡角∠ABE=45°,改造后的斜坡自動扶梯坡角∠ACB=15°,求改造后的斜坡式自動扶梯AC的長,(精確到0.1m,參考數據;sin15°≈0.26,cos15°≈0.97,tan15°≈0,27)
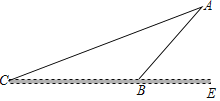
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com