
【題目】已知直線y=n與二次函數y=![]() (x﹣2)2﹣1的圖象交于點B,點C,二次函數圖象的頂點為A,當△ABC是等腰直角三角形時,則n的值為( )
(x﹣2)2﹣1的圖象交于點B,點C,二次函數圖象的頂點為A,當△ABC是等腰直角三角形時,則n的值為( )
A. 1B. ![]() C. 2﹣
C. 2﹣![]() D. 2+
D. 2+![]()
【答案】A
【解析】
設B(x1,n)、C(x2,n).因為△ABC是等腰直角三角形,作AD⊥BC,所以AD=![]() BC,即BC=2AD,AD=n﹣(﹣1)=n+1,即:BC=|x1-x2|=
BC,即BC=2AD,AD=n﹣(﹣1)=n+1,即:BC=|x1-x2|=![]() =
=![]() =
=![]() ,所以
,所以![]() =2(n+1),容易求出n=1.
=2(n+1),容易求出n=1.
設B(x1,n)、C(x2,n),作AD⊥BC,垂足為D連接AB,AC,
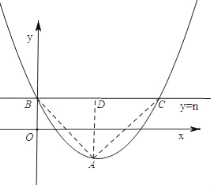
∵y=![]() (x﹣2)2﹣1,
(x﹣2)2﹣1,
∴頂點A(2,﹣1),
AD=n﹣(﹣1)=n+1
∵直線y=n與二次函數y=![]() (x﹣2)2﹣1的圖象交于點B、C,
(x﹣2)2﹣1的圖象交于點B、C,
∴![]() (x﹣2)2﹣1=n,
(x﹣2)2﹣1=n,
化簡,得x2﹣4x+2﹣2n=0,
x1+x2=4,x1x2=2﹣2n,
∴BC=|x1﹣x2|=![]() =
=![]() =
=![]() ,
,
∵點B、C關于對稱軸直線AD對稱,
∴D為線段BC的中點,
∵△ABC是等腰直角三角形,
∴AD=![]() BC,
BC,
即BC=2AD
![]() =2(n+1),
=2(n+1),
∴(2+2n)=(n+1)2,
化簡,得n2=1,
∴n=1或﹣1,
n=﹣1時直線y=n經過點A,不符合題意舍去,
所以n=1.
故選:A.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:初中數學 來源: 題型:
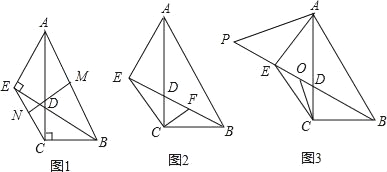
【題目】如圖1,在Rt△ABC中,∠ACB=90°,AC=2BC,點D在邊AC上,連接BD,過A作BD的垂線交BD的延長線于點E.
(1)若M,N分別為線段AB,EC的中點,如圖1,求證:MN⊥EC;
(2)如圖2,過點C作CF⊥EC交BD于點F,求證:AE=2BF;
(3)如圖3,以AE為一邊作一個角等于∠BAC,這個角的另一邊與BE的延長線交于P點,O為BP的中點,連接OC,求證:OC=![]() (BE﹣PE).
(BE﹣PE).
查看答案和解析>>
科目:初中數學 來源: 題型:
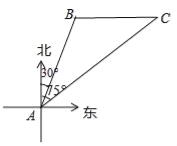
【題目】南海是我國的南大門,如圖所示,某天我國一艘海監執法船在南海海域正在進行常態化巡航,在A處測得北偏東30°方向上,距離為20海里的B處有一艘不明身份的船只正在向正東方向航行,便迅速沿北偏東75°的方向前往監視巡查,經過一段時間后,在C處成功攔截不明船只,問我海監執法船在前往監視巡查的過程中行駛了多少海里(最后結果保留整數)?
![]()
![]() (參考數據:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(參考數據:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著通訊技術迅猛發展,人與人之間的溝通方式更多樣、便捷.某校數學興趣小組設計了“你最喜歡的溝通方式”調查問卷(每人必選且只選一種),在全校范圍內隨機調查了部分學生,將統計結果繪制了如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:

(1)這次統計共抽查了 名學生;在扇形統計圖中,表示“QQ”的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整;
(3)該校共有1500名學生,請估計該校最喜歡用“微信”進行溝通的學生有多少名?
(4)某天甲、乙兩名同學都想從“微信”、“QQ”、“電話”三種溝通方式中選一種方式與對方聯系,請用列表或畫樹狀圖的方法求出甲、乙兩名同學恰好選中同一種溝通方式的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,兩個全等的△ABC和△DEF中,∠ACB=∠DFE=90°,AB=DE,其中點B和點D重合,點F在BC上,將△DEF沿射線BC平移,設平移的距離為x,平移后的圖形與△ABC重合部分的面積為y,y關于x的函數圖象如圖2所示(其中0≤x≤m,m<x≤3,3<x≤4時,函數的解析式不同)
(1)填空:BC的長為_____;
(2)求y關于x的函數關系式,并寫出x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
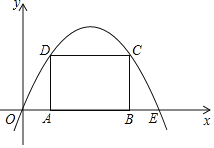
【題目】如圖,拋物線y=ax2+bx(a<0)過點E(10,0),矩形ABCD的邊AB在線段OE上(點A在點B的左邊),點C,D在拋物線上.設A(t,0),當t=2時,AD=4.
(1)求拋物線的函數表達式.
(2)當t為何值時,矩形ABCD的周長有最大值?最大值是多少?
(3)保持t=2時的矩形ABCD不動,向右平移拋物線.當平移后的拋物線與矩形的邊有兩個交點G,H,且直線GH平分矩形的面積時,求拋物線平移的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. “擲一枚硬幣正面朝上的概率是![]() ”表示每拋硬幣2次就有1次正面朝上
”表示每拋硬幣2次就有1次正面朝上
B. 一組數據2,2,3,6的眾數和中位數都是2
C. 要了解全市人民的低碳生活狀況,適宜采用抽樣調查的方法
D. 隨機抽取甲、乙兩名同學的5次數學成績,計算得平均分都是90分,方差分別是S2甲=5,S2乙=12,說明乙的成績較為穩定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學去某批零兼營的文具店,為學校美術小組的30名同學購買鉛筆和橡皮.若給全組每人各買2支鉛筆和1塊橡皮,那么需按零售價購買,共支付30元;若給全組每人各買3支鉛筆和2塊橡皮,那么可按批發價購買,共支付40.5元.已知1支鉛筆的批發價比零售價低0.05元,1塊橡皮的批發價比零售價低0.10元.請解決下列問題(均需寫出解題過程):
(1)問這家文具店每支鉛筆和每塊橡皮的批發價各是多少元?
(2)小亮同學用4元錢在這家文具店按零售價買同樣的鉛筆和橡皮(兩樣都要買,4元錢恰好用完),有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
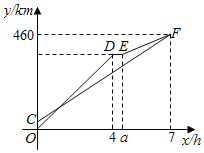
【題目】甲、乙兩車從A地出發,沿同一路線駛向B地.甲車先出發勻速駛向B地,40min后,乙車出發,勻速行駛一段時間后,在途中的貨站裝貨耗時半小時.由于滿載貨物,為了行駛安全,速度減少了50km/h,結果與甲車同時到達B地,甲乙兩車距A地的路程![]() (
(![]() )與乙車行駛時間
)與乙車行駛時間![]() (
(![]() )之間的函數圖象如圖所示,則下列說法:①
)之間的函數圖象如圖所示,則下列說法:①![]() ②甲的速度是60km/h;③乙出發80min追上甲;④乙車在貨站裝好貨準備離開時,甲車距B地150km;⑤當甲乙兩車相距30 km時,甲的行駛時間為1 h、3 h、
②甲的速度是60km/h;③乙出發80min追上甲;④乙車在貨站裝好貨準備離開時,甲車距B地150km;⑤當甲乙兩車相距30 km時,甲的行駛時間為1 h、3 h、![]() h;其中正確的是__________.
h;其中正確的是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com