
【題目】在平面直角坐標(biāo)系中,如果直線(xiàn) y=kx 與函數(shù) y= 的圖象恰有 3 個(gè)不同的交點(diǎn),則 k的取值范圍是_________.
的圖象恰有 3 個(gè)不同的交點(diǎn),則 k的取值范圍是_________.
【答案】![]() <k<2
<k<2
【解析】
根據(jù)題意把y=kx分別代入各個(gè)分段函數(shù)解析式,用k表示出x的值,再根據(jù)x的取值范圍確定k的范圍.
解:①∵直線(xiàn)y=kx與函數(shù)y=2x+4有交點(diǎn),
∴kx=2x+4,
∴x=![]() ,
,
又∵x<﹣3,
即![]() ,
,
當(dāng)k﹣2>0,即k>2時(shí),解得k![]() ,
,
此時(shí)無(wú)解.
當(dāng)k﹣2<0,即k<2時(shí),解得k![]() ,
,
∴![]() ,
,
②∵直線(xiàn)y=kx與函數(shù)y=﹣2有交點(diǎn),
∴kx=﹣2,
∴x=![]() ,
,
又∵﹣3≤x≤3,
即﹣3≤![]() ≤3,
≤3,
解得:k![]() ,
,
③∵直線(xiàn)y=kx與函數(shù)y=2x﹣8有交點(diǎn),
∴kx=2x﹣8,
∴x=![]() ,
,
又∵x>3,
即![]() ,
,
解得:k![]() ,
,
綜上所述:![]() .
.
故答案為:![]() <k<2.
<k<2.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知關(guān)于x的函數(shù)y=k(x﹣1)和![]() (k≠0),它們?cè)谕蛔鴺?biāo)系內(nèi)的圖象大致是( )
(k≠0),它們?cè)谕蛔鴺?biāo)系內(nèi)的圖象大致是( )
A. 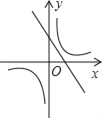 B.
B. 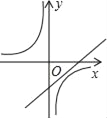 C.
C. 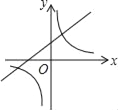 D.
D. 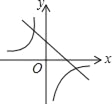
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
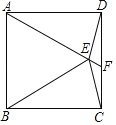
【題目】如圖,在正方形ABCD中,△ABE為等邊三角形,連接DE,CE,延長(zhǎng)AE交CD于F點(diǎn),則∠DEF的度數(shù)為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】均勻的正四面體的各面依次標(biāo)有![]() 四個(gè)數(shù)字
四個(gè)數(shù)字![]() 小明做了60次投擲試驗(yàn),結(jié)果統(tǒng)計(jì)如下:
小明做了60次投擲試驗(yàn),結(jié)果統(tǒng)計(jì)如下:
朝下數(shù)字 | 1 | 2 | 3 | 4 |
出現(xiàn)的次數(shù) | 16 | 20 | 14 | 10 |
![]() 計(jì)算上述試驗(yàn)中“4朝下”的頻率是多少?
計(jì)算上述試驗(yàn)中“4朝下”的頻率是多少?
![]() “根據(jù)試驗(yàn)結(jié)果,投擲一次正四面體,出現(xiàn)2朝下的概率是
“根據(jù)試驗(yàn)結(jié)果,投擲一次正四面體,出現(xiàn)2朝下的概率是![]() ”的說(shuō)法正確嗎?為什么?
”的說(shuō)法正確嗎?為什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
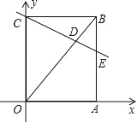
【題目】如圖,在直角坐標(biāo)系中,矩形 ABCO 的邊 OA 在 x 軸上,邊 OC 在 y 軸上,點(diǎn) B 的坐標(biāo)為(3,4),直線(xiàn) CD 分別交 OB、AB 于點(diǎn) D、E,若 BD=BE,則點(diǎn) D 的坐標(biāo)為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
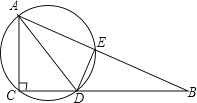
【題目】如圖,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,過(guò)A,C,D三點(diǎn)的圓與斜邊AB交于點(diǎn)E,連接DE.
(1)求證:AC=AE;
(2)若AC=6,CB=8,求△ACD外接圓的直徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正五邊形ABCDE中,對(duì)角線(xiàn)![]() 與EB分別相交于點(diǎn)
與EB分別相交于點(diǎn)![]() 下列結(jié)論錯(cuò)誤的是
下列結(jié)論錯(cuò)誤的是![]()
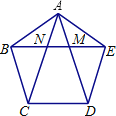
A. 四邊形EDCN是菱形
B. 四邊形MNCD是等腰梯形
C. ![]() 與
與![]() 相似
相似
D. ![]() 與
與![]() 全等
全等
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線(xiàn)![]() (a≠0)的對(duì)稱(chēng)軸為直線(xiàn)x=1,與x軸的一個(gè)交點(diǎn)坐標(biāo)為(﹣1,0),其部分圖象如圖所示,下列結(jié)論:
(a≠0)的對(duì)稱(chēng)軸為直線(xiàn)x=1,與x軸的一個(gè)交點(diǎn)坐標(biāo)為(﹣1,0),其部分圖象如圖所示,下列結(jié)論:
①4ac<b2;
②方程![]() 的兩個(gè)根是x1=﹣1,x2=3;
的兩個(gè)根是x1=﹣1,x2=3;
③3a+c>0
④當(dāng)y>0時(shí),x的取值范圍是﹣1≤x<3
⑤當(dāng)x<0時(shí),y隨x增大而增大
其中結(jié)論正確的個(gè)數(shù)是( )

A. 4個(gè) B. 3個(gè) C. 2個(gè) D. 1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知:![]() ,
,![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 三點(diǎn)在一直線(xiàn)上,請(qǐng)?zhí)顚?xiě)
三點(diǎn)在一直線(xiàn)上,請(qǐng)?zhí)顚?xiě)![]() 的理由.
的理由.

解:在![]() 與
與![]() 中,
中,
![]() (已知),
(已知),
![]() (已知),
(已知),
![]() (已知),
(已知),
所以![]()
所以![]()
![]() ________(________)
________(________)
所以![]() (等式性質(zhì)),
(等式性質(zhì)),
即![]() ________
________![]() ________.
________.
因?yàn)?/span>![]() (________)
(________)
即![]() ,
,
所以![]() (________).
(________).
所以![]() (等量代換).
(等量代換).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com