
【題目】如圖1,小紅將一張直角梯形紙片沿虛線剪開,得到矩形和三角形兩張紙片,測得AB=15,AD=12.在進行如下操作時遇到了下面的幾個問題,請你幫助解決.
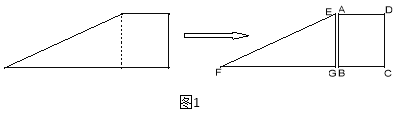
(1)將△EFG的頂點G移到矩形的頂點B處,再將三角形繞點B順時針旋轉使E點落在CD邊上,此時,EF恰好經過點A(如圖2)求FB的長度
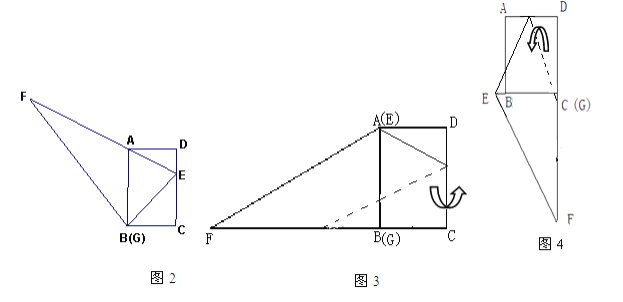
(2)在(1)的條件下,小紅想用△EFG包裹矩形ABCD,她想了兩種包裹的方法如圖3、圖4,請問哪種包裹紙片的方法使得未包裹住的面積大?(紙片厚度忽略不計)請你通過計算說服小紅。
【答案】(1)30;(2) 二種包裹紙片的方法使得未包裹住的面積相等.
【解析】
試題分析:(1)利用矩形的性質以及得出△ADE∽△FBE,求出即可;
(2)根據Rt△F,HN~Rt△F,EG,得到HN=3,從而S△AMH=144;由Rt△GBE~Rt△C,B,G,得到GB,=24,從而S△B,C,G=144,進行比較即可.
⑴BE=AD=15,在RtBCE中,CE2=B E2-BC2=152-122,求得CE=9,DE=6,
證Rt△ADE~Rt△FBE,
求得BF=30
⑵①如圖1,將矩形ABCD和Rt△FBE以CD為軸翻折,則△AMH即為未包裹住的面積,

由Rt△F,HN~Rt△F,EG,得到HN=3,
從而S△AMH=144
②如圖2,將矩形ABCD和Rt△ECF以AD為軸翻折,由Rt△GBE~Rt△C,B,G,得到GB,=24,

從而S△B,C,G=144,∴未包裹的面積為144.
∴按照二種包裹的方法未包裹的面積相等。


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案科目:初中數學 來源: 題型:
【題目】一根祝壽蠟燭長85 cm,點燃時每小時縮短5 cm.
(1)請寫出點燃蠟燭的長y(cm)與蠟燭燃燒時間t(h)之間的函數關系式;
(2)該蠟燭可點燃多長時間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實踐與探索:將連續的奇數1,3,5,7…排列成如圖的數表用十字框框出5個數(如圖) 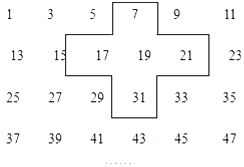
(1)若將十字框上下左右平移,但一定要框住數列中的5個數,若設中間的數為a,用a的代數式表示十字框框住的5個數字之和;
(2)十字框框住的5個數之和能等于2015嗎?若能,分別寫出十字框框住的5個數;若不能,請說明理由;
(3)十字框框住的5個數之和能等于365嗎?若能,分別寫出十字框框住的5個數;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ACE是以□ABCD的對角線AC為邊的等邊三角形,點C與點E關于x軸對稱.若E點的坐標是(7,-3 ![]() ),則D點的坐標是 ( )
),則D點的坐標是 ( )
A.(4,0)
B.( ![]() ,0)
,0)
C.(5,0)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,①②③④⑤五個平行四邊形拼成一個含30度內角的菱形EFGH(不重疊無縫隙).若①②③④四個平行四邊形面積的和為26cm2 , 四邊形ABCD面積是19cm2 , 則①②③④四個平行四邊形周長的總和為( )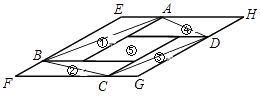
A.96cm
B.64cm
C.48cm
D.36cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(-1,0),點B的坐標為(4,0),經過點A點B拋物線y=x+bx+c與y軸交于點C.
(1)求拋物線的關系式.
(2)△ABC的外接圓與y軸交于點D,在拋物線上是否存在點M使S△MBC=S△DBC,若存在,請求出點M的坐標.
(3)點P是直線y=-x上一個動點,連接PB,PC,當PB+PC+PO最小時,求點P的坐標及其最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A是y軸正半軸上的一個定點,點B是反比例函數y=![]() (k為常數)在第一象限內圖象上的一個動點.當點B的縱坐標逐漸增大時,△OAB的面積( )
(k為常數)在第一象限內圖象上的一個動點.當點B的縱坐標逐漸增大時,△OAB的面積( )
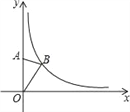
A. 逐漸減小 B. 逐漸增大 C. 先增大后減小 D. 不變
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com