
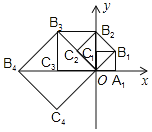
【題目】如圖,在平面直角坐標系中,邊長為1的正方形![]() 的兩邊在坐標軸上,以它的對角線
的兩邊在坐標軸上,以它的對角線![]() 為邊作正方形
為邊作正方形![]() ,再以正方形
,再以正方形![]() 的對角線
的對角線![]() 為邊作正方形
為邊作正方形![]() ,以此類推
,以此類推![]() 、則正方形
、則正方形![]() 的頂點
的頂點![]() 的坐標是______.
的坐標是______.
 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:初中數學 來源: 題型:
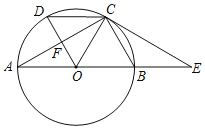
【題目】如圖,已知![]() 為
為![]() 的直徑,
的直徑,![]() ,點
,點![]() 和點
和點![]() 是
是![]() 上關于直線
上關于直線![]() 對稱的兩個點,連接
對稱的兩個點,連接![]() 、
、![]() ,且
,且![]() ,直線
,直線![]() 和直線
和直線![]() 相交于點
相交于點![]() ,過點
,過點![]() 作直線
作直線![]() 與線段
與線段![]() 的延長線相交于點
的延長線相交于點![]() ,與直線
,與直線![]() 相交于點
相交于點![]() ,且
,且![]() .
.

(1)求證:直線![]() 為
為![]() 的切線;
的切線;
(2)若點![]() 為線段
為線段![]() 上一點,連接
上一點,連接![]() ,滿足
,滿足![]() ,
,
①求證:![]() ;
;
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】AB是⊙O的直徑,C點在⊙O上,F是AC的中點,OF的延長線交⊙O于點D,點E在AB的延長線上,∠A=∠BCE.
(1)求證:CE是⊙O的切線;
(2)若BC=BE,判定四邊形OBCD的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
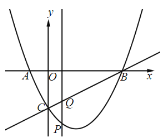
【題目】如圖,在平面直角坐標系中,拋物線![]() 過點
過點![]() ,
,![]() ,與
,與![]() 軸交于點
軸交于點![]() .點
.點![]() 是
是![]() 軸下方的拋物線上一動點(包含點
軸下方的拋物線上一動點(包含點![]() ,
,![]() ).作直線
).作直線![]() ,若過點
,若過點![]() 作
作![]() 軸的垂線,交直線
軸的垂線,交直線![]() 于點
于點![]() .
.
(1)求拋物線的解析式;
(2)在點![]() 運動的過程中,請求出
運動的過程中,請求出![]() 面積的最大值及此時點
面積的最大值及此時點![]() 的坐標;
的坐標;
(3)在點![]() 運動的過程中,是否存在點
運動的過程中,是否存在點![]() ,使
,使![]() 是等腰三角形.若存在,請直接寫出點
是等腰三角形.若存在,請直接寫出點![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的四個頂點分別在反比例函數![]() 與
與![]() (x>0,0<m<n)的圖象上,對角線BD//y軸,且BD⊥AC于點P.已知點B的橫坐標為4.
(x>0,0<m<n)的圖象上,對角線BD//y軸,且BD⊥AC于點P.已知點B的橫坐標為4.
(1)當m=4,n=20時.
①若點P的縱坐標為2,求直線AB的函數表達式.
②若點P是BD的中點,試判斷四邊形ABCD的形狀,并說明理由.
(2)四邊形ABCD能否成為正方形?若能,求此時m,n之間的數量關系;若不能,試說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】盒中有x個黑球和y個白球,這些球除顏色外無其他差別.若從盒中隨機取一個球,它是黑球的 概率是![]() ;中再放進1個黑球,這時取得黑球的概率變為
;中再放進1個黑球,這時取得黑球的概率變為![]()
(1)填空:x=_____________, y=____________________;
(2)小王和小林利用x黑球和y個白球進行摸球游戲。約定:從盒中隨機摸取一個,接著從剩下的球中再隨機摸取一個,若兩球顏色相同則小王勝,若顏色不同則小林勝.求兩個人獲勝的概率各是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
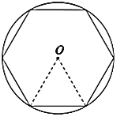
【題目】中國魏晉時期的數學家劉徽首創“割圓術”,奠定了中國圓周率計算在世界上的領先地位.劉徽提出:“割之彌細,所失彌少,割之又割,以至于不可割,則與圓周合體,而無所失矣”,由此求得圓周率![]() 的近似值.如圖,設半徑為
的近似值.如圖,設半徑為![]() 的圓內接正
的圓內接正![]() 邊形的周長為
邊形的周長為![]() ,圓的直徑為
,圓的直徑為![]() ,當
,當![]() 時,
時,![]() ,則當
,則當![]() 時,
時,![]() ______.(結果精確到0.01,參考數據:
______.(結果精確到0.01,參考數據:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AM∥BN,C是BN上一點, BD平分∠ABN且過AC的中點O,交AM于點D,DE⊥BD,交BN于點E.
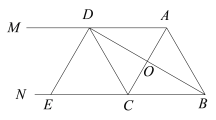
(1)求證:△ADO≌△CBO.
(2)求證:四邊形ABCD是菱形.
(3)若DE = AB = 2,求菱形ABCD的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一不透明的袋子中裝有四張標有數字![]() 的卡片,這些卡片除數字外其余均相同.小明同學按照一定的規則抽出兩張卡片,并把卡片上的數字相加,下圖是他所畫的樹狀圖的一部分.
的卡片,這些卡片除數字外其余均相同.小明同學按照一定的規則抽出兩張卡片,并把卡片上的數字相加,下圖是他所畫的樹狀圖的一部分.
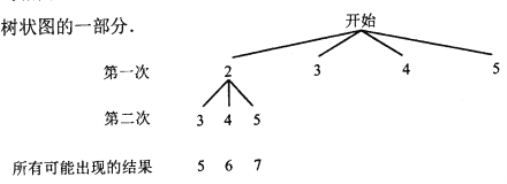
(1)由上圖分析,該游戲規則是:第一次從袋子中隨機抽出一張卡片后 (填“放回”或“不放回”),第二次隨機再抽出一張卡片;
(2)幫小明同學補全樹狀圖,并求小明同學兩次抽到卡片上的數字之和為偶數的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com