【題目】已知二次函數y=ax2+bx+c（a≠0）的圖象如圖所示，下列結論：①2a+b＜0；②abc＜0；③b2﹣4ac＞0；④a+b+c＜0；⑤（a﹣2b+c）＜0，其中正確的個數是（ ）
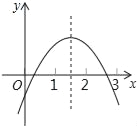
A. 2 B. 3 C. 4 D. 5
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：初中數學 來源： 題型：
【題目】如圖，將一張正方形紙片ABCD對折，使CD與AB重合，得到折痕MN后展開，E為CN上一點，將△CDE沿DE所在的直線折疊，使得點C落在折痕MN上的點F處，連接AF，BF，BD.則下列結論中：①△ADF是等邊三角形；②tan∠EBF＝2－
；③S△ADF＝
S正方形ABCD；④BF2＝DF·EF.其中正確的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在兩建筑物之間有一旗桿，高15米，從A點經過旗桿頂點恰好看到矮建筑物的墻角C點，且俯角α為60°，又從A點測得D點的俯角β為30°，若旗桿底點G為BC的中點，則矮建筑物的高CD為（ ）
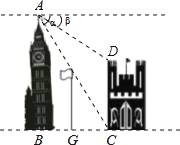
A. 20米 B. 
米 C. 
米 D. 
米
查看答案和解析>>
科目：初中數學 來源： 題型：
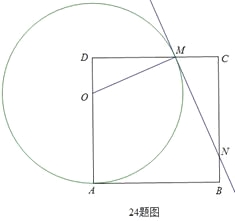
【題目】如圖，在邊長為8的正方形ABCD中，點O為AD上一動點（4＜OA＜8），以O為圓心，OA的長為半徑的圓交邊CD于點M，連接OM，過點M作圓O的切線交邊BC于點N.
（1）求證：△ODM∽△MCN；
（2）設DM=x，求OA的長（用含x的代數式表示）；
（3）在點O運動的過程中，設△CMN的周長為p，試用含x的代數式表示p，你能發現怎樣的結論？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，∠CAB=90°，AD⊥BC于點D，點E為AB的中點，EC與AD交于點G，點F在BC上．
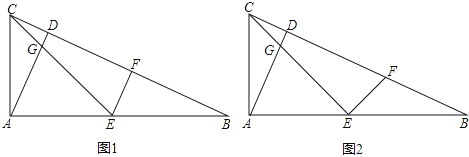
（1）如圖1，AC：AB=1：2，EF⊥CB，求證：EF=CD．
（2）如圖2，AC：AB=1：
，EF⊥CE，求EF：EG的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線y=x2+bx+c與y軸交于點A（0，2），對稱軸為直線x=﹣2，平行于x軸的直線與拋物線交于B、C兩點，點B在對稱軸左側，BC=6．
（1）求此拋物線的解析式．
（2）點P在x軸上，直線CP將△ABC面積分成2：3兩部分，請直接寫出P點坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，∠C=90°，∠ABC的平分線BE交AC于點E，過點E作直線BE的垂線交AB于點F，⊙O是△BEF的外接圓．
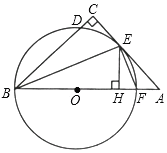
（1）求證：AC是⊙O的切線；
（2）過點E作EH⊥AB于點H，求證：EF平分∠AEH；
（3）求證：CD=HF．
查看答案和解析>>
科目：初中數學 來源： 題型：
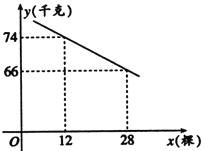
【題目】小麗老師家有一片80棵桃樹的桃園，現準備多種一些桃樹提高桃園產量，但是如果多種樹，那么樹之間的距離和每棵樹所受光照就會減少，單棵樹的產量隨之降低.若該桃園每棵桃樹產桃
(千克)與增種桃樹
(棵)之間的函數關系如圖所示.
(1)求與之間的函數關系式;
(2)在投入成本最低的情況下，增種桃樹多少棵時，桃園的總產量可以達到6750千克?
(3)如果增種的桃樹 (棵)滿足: 
，請你幫小麗老師家計算一下，桃園的總產量最少是多少千克，最多又是多少千克?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在△ABC中，AB=AC，AB的垂直平分線DE與AC所在的直線相交于點E，垂足為D，連接BE．已知AE=5，tan∠AED=
，求BE+CE的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
