
【題目】解下列方程:
(1)![]() x22x7=0
x22x7=0
(2)![]() 2(x1)2=1x
2(x1)2=1x
【答案】
(1)解:∵ x22x=7,
∴x22x+1=7+1,
即(x1)2=8,
∴x1=2![]() 或x1=-2
或x1=-2![]() ,
,
即x1=1+2![]() ,x2=12
,x2=12![]() .
.
(2)解:∵ 2(x1)2=(x1),
∴2(x1)2+(x1)=0,
∴(x1)[2(x1)+1]=0,
∴x1=0或2(x1)+1=0,
∴x1=1,x2=![]() .
.
【解析】(1)根據配方法和直接開平方法即可解方程.
(2)根據因式分解——提公因式法即可解方程.
【考點精析】利用直接開平方法和配方法對題目進行判斷即可得到答案,需要熟知方程沒有一次項,直接開方最理想.如果缺少常數項,因式分解沒商量.b、c相等都為零,等根是零不要忘.b、c同時不為零,因式分解或配方,也可直接套公式,因題而異擇良方;左未右已先分離,二系化“1”是其次.一系折半再平方,兩邊同加沒問題.左邊分解右合并,直接開方去解題.


科目:初中數學 來源: 題型:
【題目】列方程解應用題:
某玩具廠生產一種玩具,按照控制固定成本降價促銷的原則,使生產的玩具能夠及時售出,據市場調查:每個玩具按![]() 元銷售時,每天可銷售
元銷售時,每天可銷售![]() 個;若銷售單價每降低元,每天可多售出
個;若銷售單價每降低元,每天可多售出![]() 個.已知每個玩具的固定成本為
個.已知每個玩具的固定成本為![]() 元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤
元,問這種玩具的銷售單價為多少元時,廠家每天可獲利潤![]() 元?
元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在線段AB上,點M、N分別是AC、BC的中點.
![]()
![]() 若
若![]() ,求線段MN的長;
,求線段MN的長;
![]() 若C為線段AB上任一點,滿足
若C為線段AB上任一點,滿足![]() ,其它條件不變,你能猜想MN的長度嗎?并說明理由,你能用一句簡潔的話描述你發現的結論嗎?
,其它條件不變,你能猜想MN的長度嗎?并說明理由,你能用一句簡潔的話描述你發現的結論嗎?
![]() 若C在線段AB的延長線上,且滿足
若C在線段AB的延長線上,且滿足![]() cm,M、N分別為AC、BC的中點,你能猜想MN的長度嗎?請畫出圖形,寫出你的結論,并說明理由.
cm,M、N分別為AC、BC的中點,你能猜想MN的長度嗎?請畫出圖形,寫出你的結論,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
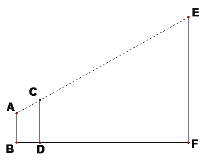
【題目】(1)在一次測量旗桿高度的活動中,某小組使用的方案如下:AB表示某同學從眼睛到腳底的距離,CD表示一根標桿,EF表示旗桿,AB、CD、EF都垂直于地面。若AB=1.6m,CD=2m,人與標桿之間的距離BD=1m,標桿與旗桿之間的距離DF=30m,求旗桿EF的高度。
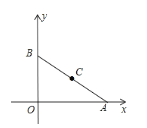
(2)如圖在平面直角坐標系中,A點坐標為(8,0),B點坐標為(0,6),點C是線段AB的中點。請問在x軸上是否存在一點P,使得以P、A、C為頂點的三角形與△AOB相似?若存在,求出P點坐標(寫出計算的過程);若不存在,說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,D是AC上一點,E是AB上一點,且∠AED=∠C.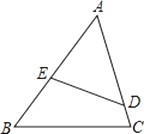
(1)求證:△AED∽△ACB;
(2)若AB=6,AD=4,AC=5,求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com