
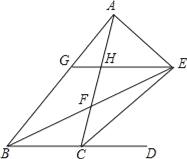
【題目】如圖,△ABC的內角∠ABC和外角∠ACD的平分線相交于點E,BE交AC于點F,過點E作EG∥BD交AB于點G,交AC于點H,連接AE,有以下結論:
①∠BEC=![]() ∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正確的結論有_____(將所有正確答案的序號填寫在橫線上).
∠BAC;②△HEF≌△CBF;③BG=CH+GH;④∠AEB+∠ACE=90°,其中正確的結論有_____(將所有正確答案的序號填寫在橫線上).
【答案】①③④.
【解析】
①根據角平分線的定義得到∠EBC=![]() ∠ABC,∠DCE=
∠ABC,∠DCE=![]() ∠ACD,根據外角的性質即可得到結論;
∠ACD,根據外角的性質即可得到結論;
②根據相似三角形的判定定理得到兩個三角形相似,不能得出全等;
③由BG=GE,CH=EH,于是得到BG-CH=GE-EH=GH.即可得到結論;
④由于E是兩條角平分線的交點,根據角平分線的性質可得出點E到BA、AC、BC和距離相等,從而得出AE為∠BAC外角平分線這個重要結論,再利用三角形內角和性質與外角性質進行角度的推導即可輕松得出結論.
①BE平分∠ABC,
∴∠EBC=![]() ∠ABC,
∠ABC,
∵CE平分∠ACD,
∴∠DCE=![]() ∠ACD,
∠ACD,
∵∠ACD=∠BAC+∠ABC,∠DCE=∠CBE+∠BEC,
∴∠EBC+∠BEC=![]() (∠BAC+∠ABC)=∠EBC+
(∠BAC+∠ABC)=∠EBC+![]() ∠BAC,
∠BAC,
∴∠BEC=![]() ∠BAC,故①正確;
∠BAC,故①正確;
∵②△HEF與△CBF只有兩個角是相等的,能得出相似,但不含相等的邊,所以不能得出全等的結論,故②錯誤;
③BE平分∠ABC,
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,
同理CH=HE,
∴BGCH=GEEH=GH,
∴BG=CH+GH,
故③正確;
④過點E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如圖,
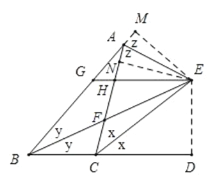
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
設∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如圖,
則∠BAC=180![]() 2z,∠ACB=180
2z,∠ACB=180![]() 2x,
2x,
∵∠ABC+∠ACB+∠BAC=180![]() ,
,
∴2y+180![]() 2z+180
2z+180![]() 2x=180
2x=180![]() ,
,
∴x+z=y+90![]() ,
,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90![]() ,
,
∴x+∠AEB=90![]() ,
,
即∠ACE+∠AEB=90![]() ,
,
故④正確.
故答案為:①③④.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某村計劃對總長為1800m的道路進行改造,安排甲、乙兩個工程隊完成![]() 已知甲隊每天能完成的道路長度是乙隊每天能完成的2倍,并且在獨立完成長為400m的道路時,甲隊比乙隊少用4天.
已知甲隊每天能完成的道路長度是乙隊每天能完成的2倍,并且在獨立完成長為400m的道路時,甲隊比乙隊少用4天.
![]() 求甲、乙兩工程隊每天能完成道路的長度分別是多少m?
求甲、乙兩工程隊每天能完成道路的長度分別是多少m?
![]() 若村委每天需付給甲隊的道路改造費用為
若村委每天需付給甲隊的道路改造費用為![]() 萬元,乙隊為
萬元,乙隊為![]() 萬元,要使這次的道路改造費用不超過8萬元,至少應安排甲隊工作多少天?
萬元,要使這次的道路改造費用不超過8萬元,至少應安排甲隊工作多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC 
(1)求證:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度數;
(3)若AD=3,AB=4,求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:![]() =
=![]() (a≠0),即a的負P次冪等于a的p次冪的倒數.例:
(a≠0),即a的負P次冪等于a的p次冪的倒數.例:![]() =
=![]()
(1)計算:![]() =__;
=__;![]() =__;
=__;
(2)如果![]() =
=![]() ,那么p=__;如果
,那么p=__;如果![]() =
=![]() ,那么a=__;
,那么a=__;
(3)如果![]() =
=![]() ,且a、p為整數,求滿足條件的a、p的取值.
,且a、p為整數,求滿足條件的a、p的取值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中有一個軸對稱圖形,A(3,-2),B(3,﹣6)兩點在此圖形上且互為對稱點,若此圖形上有一個點C(﹣2,+1).
(1)求點C的對稱點的坐標.
(2)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某高樓頂部有一信號發射塔,在矩形建筑物ABCD的A、C兩點測得該塔頂端F的仰角分別為45°和60°,矩形建筑物寬度AD=20m,高度DC=30m則信號發射塔頂端到地面的高度(即FG的長)為( )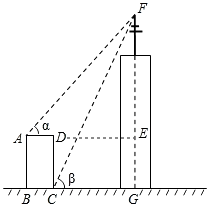
A.(35 ![]() +55)m
+55)m
B.(25 ![]() +45)m
+45)m
C.(25 ![]() +75)m
+75)m
D.(50+20 ![]() )m
)m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AB的垂直平分線DE交AC于D,垂足為E,若∠A=30°,CD=3.

(1)求∠BDC的度數.
(2)求AC的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com