
【題目】某校組織數學興趣探究活動,愛思考的小實同學在探究兩條直線的位置關系查閱資料時發現,兩條中線互相垂直的三角形稱為“中垂三角形”.如圖1、圖2、圖3中,![]() 、
、![]() 是
是![]() 的中線,
的中線,![]() 于點
于點![]() ,像
,像![]() 這樣的三角形均稱為“中垂三角形”.
這樣的三角形均稱為“中垂三角形”.
(特例探究)
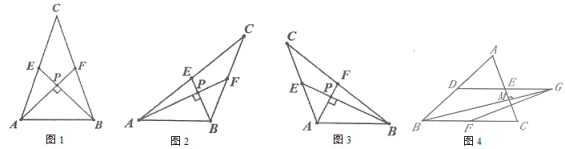
(1)如圖1,當![]() ,
,![]() 時,
時,![]() _____,
_____,![]() ______;
______;
如圖2,當![]() ,
,![]() 時,
時,![]() _____,
_____,![]() ______;
______;
(歸納證明)
(2)請你觀察(1)中的計算結果,猜想![]() 、
、![]() 、
、![]() 三者之間的關系,用等式表示出來,并利用圖3證明你的結論;
三者之間的關系,用等式表示出來,并利用圖3證明你的結論;
(拓展證明)
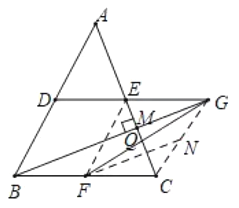
(3)如圖4,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]()
![]() 的中點,連結
的中點,連結![]() 并延長至
并延長至![]() ,使得
,使得![]() ,連結
,連結![]() ,當
,當![]() 于點
于點![]() 時,求
時,求![]() 的長.
的長.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ,證明見解析;(3)
,證明見解析;(3)![]() .
.
【解析】
(1)由三角函數的性質得到![]() 根據三角形中位線的性質,得到EF//AB.
根據三角形中位線的性質,得到EF//AB. ![]() ,由平行線分線段成比例可得
,由平行線分線段成比例可得![]() ,可求得PE、PE的長,再由勾股定理得到結果;由三角函數的性質得到
,可求得PE、PE的長,再由勾股定理得到結果;由三角函數的性質得到![]() 根據三角形中位線的性質,得到EF//AB.
根據三角形中位線的性質,得到EF//AB. ![]() ,由平行線分線段成比例可得
,由平行線分線段成比例可得![]() ,可求得PE、PE的長再由勾股定理得到結果;
,可求得PE、PE的長再由勾股定理得到結果;
(2) 設![]() ,
,![]() ,則
,則![]() ,
,![]() ,利用勾股定理用x、y、z分別表示出:
,利用勾股定理用x、y、z分別表示出:![]() 、
、![]() 、
、![]() ,再用x、y、z分別表示出
,再用x、y、z分別表示出![]() ,
,![]() ,由
,由![]() 即可得出答案;
即可得出答案;
(3)連結![]() ,
,![]() 過點
過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,可得四邊形
,可得四邊形![]() 是平行四邊形,可得
是平行四邊形,可得![]() 是中垂三角形,即可知:
是中垂三角形,即可知:![]() ,
,![]() 代入(2)中結論可求得
代入(2)中結論可求得![]()
(1)解:如圖,連接EF
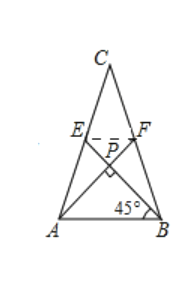
∵![]() ,
,![]() ,
,![]()
∴![]()
∵![]() 、
、![]() 是
是![]() 的中線,
的中線,![]() 是交點
是交點
∴![]()
∴![]()
∴![]()
∵![]()
∴由勾股定理可得:![]()
∴![]()
如圖連接EF
∵![]() ,
,![]() ,
,![]()
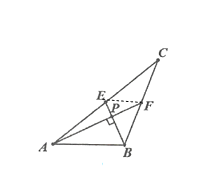
∴![]() ,
,![]()
∵![]() 、
、![]() 是
是![]() 的中線,
的中線,![]() 是交點
是交點
∴![]()
∴![]()
∴![]() ,
,![]()
∵![]()
∴由勾股定理可得:![]() ,
,![]()
∴![]() ,
,![]()
故答案為:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)![]() ,理由如下:
,理由如下:
設![]() ,
,![]() ,則
,則![]() ,
,![]()
∵![]()
∴![]()
![]()
![]()
∴![]() ,
,
![]()
∴![]()
即![]()
(3)連結![]() ,
,![]() 過點
過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,
,
∵![]() ,
,![]()
∴![]()
∵![]() 是
是![]() 的中點
的中點
∴![]() 是
是![]() 的中點
的中點
∵![]() ,
,![]() 是
是![]() ,
,![]() 的中點
的中點
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴四邊形![]() 是平行四邊形
是平行四邊形
∴![]() 是
是![]() 的中點
的中點
∴![]() 是中垂三角形
是中垂三角形
∵![]() ,
,![]() ,
,
∴![]() ,
,![]()
有(2)中結論可知:![]()
∴![]()


科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
(1)請畫出將△ABC向左平移4個單位長度后得到的圖形△A1B1C1;
(2)請畫出△ABC關于原點O成中心對稱的圖形△A2B2C2;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
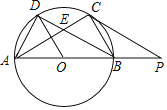
【題目】如圖,AB是⊙O的直徑,弦AC與BD交于點E,且AC=BD,連接AD,BC.
(1)求證:△ADB≌△BCA;
(2)若OD⊥AC,AB=4,求弦AC的長;
(3)在(2)的條件下,延長AB至點P,使BP=2,連接PC.求證:PC是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我校八年級有800名學生,在體育中考前進行一次排球模擬測試,從中隨機抽取部分學生,根據其測試成績制作了下面兩個統計圖,請根據相關信息,解答下列問題:

(1)本次抽取到的學生人數為________,圖2中![]() 的值為_________.
的值為_________.
(2)本次調查獲取的樣本數據的平均數是__________,眾數是________,中位數是_________.
(3)根據樣本數據,估計我校八年級模擬體測中得12分的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() (b,c為常數).
(b,c為常數).
(1)若拋物線的頂點坐標為(1,1),求b,c的值;
(2)若拋物線上始終存在不重合的兩點關于原點對稱,求c的取值范圍;
(3)在(1)的條件下,存在正實數m,n( m<n),當m≤x≤n時,恰好有![]() ,求m,n的值.
,求m,n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,并且關于x的一元二次方程ax2+bx+c﹣m=0有兩個不相等的實數根,下列結論:①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,其中,正確的個數有( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
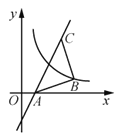
【題目】如圖,過點C(3,4)的直線![]() 交
交![]() 軸于點A,∠ABC=90°,AB=CB,曲線
軸于點A,∠ABC=90°,AB=CB,曲線![]() 過點B,將點A沿
過點B,將點A沿![]() 軸正方向平移
軸正方向平移![]() 個單位長度恰好落在該曲線上,則
個單位長度恰好落在該曲線上,則![]() 的值為________.
的值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
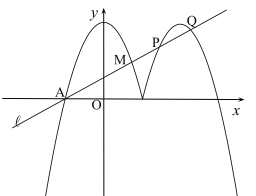
【題目】在平面直角坐標系中,拋物線![]() 的最高點的縱坐標是2.
的最高點的縱坐標是2.
(1)求拋物線的表達式;
(2)將拋物線在![]() 之間的部分記為圖象
之間的部分記為圖象![]() ,將圖象
,將圖象![]() 沿直線x=1翻折,翻折后圖象記為
沿直線x=1翻折,翻折后圖象記為![]() ,圖象
,圖象![]() 和
和![]() 組成G,直線
組成G,直線![]() :
:![]()
![]() 和圖象G在x軸上方的部分有兩個公共點,求k的取值范圍;
和圖象G在x軸上方的部分有兩個公共點,求k的取值范圍;
(3)直線![]() :
:![]() 與圖象G在x軸上方的部分分別交于A、M、P、Q四點,若AM=2PQ,求
與圖象G在x軸上方的部分分別交于A、M、P、Q四點,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com