
【題目】將一個矩形紙片![]() 放置在平面直角坐標系
放置在平面直角坐標系![]() 內,點
內,點![]() ,點
,點![]() ,點
,點![]() .點
.點![]() 是線段
是線段![]() 上的動點,將
上的動點,將![]() 沿
沿![]() 翻折得到
翻折得到![]() .
.
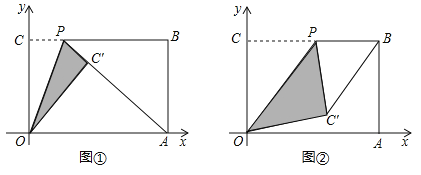
(Ⅰ)如圖①,當點![]() 落在線段
落在線段![]() 上時,求點
上時,求點![]() 的坐標;
的坐標;
(Ⅱ)如圖②,當點![]() 為線段
為線段![]() 中點時,求線段
中點時,求線段![]() 的長度;
的長度;
【答案】(Ⅰ)P(62![]() ,4)(Ⅱ)
,4)(Ⅱ)![]()
【解析】
(Ⅰ)如圖①,證明AO=AP=6,利用勾股定理求出PB即求出點P的坐標.
(Ⅱ)如圖②,連接CC′交OP于D.解直角三角形求出PD,利用三角形的中位線定理即可解決問題.
(Ⅰ)∵點![]() ,點
,點![]() ,
,
∴OA=6,OC=4,
由翻折可知:∠OPC=∠OPA,
∵BC∥OA,
∴∠OPC=∠OPA,
∴∠POA=∠OPA,
∴OA=PA=6,
在Rt△PAB中,
∵∠B=90![]() ,AB=4,PA=6,
,AB=4,PA=6,
∴PB=![]() =
=![]() ,
,
∴PC=BCPB=62![]() ,
,
∴P(62![]() ,4).
,4).
(Ⅱ)如圖②,連接CC′交OP于D.

在Rt△OPC中,∵OC=4,PC=3,
∴OP=![]() ,
,
∵OP垂直平分線段CC′,
又∵![]() OPCD=
OPCD=![]() OCPC,
OCPC,
∴CD=![]() =
=![]() ,PD=
,PD=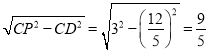
∵PC=PB,CD=DC′,
∴BC′=2PD=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC=5,BC=6,AD是BC邊上的中線,四邊形ADBE是平行四邊形.
(1)求證:四邊形ADBE是矩形;
(2)求矩形ADBE的面積.
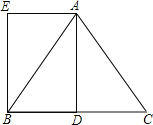
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】M(﹣1,![]() ),N(1,
),N(1,![]() )是平面直角坐標系xOy中的兩點,若平面內直線MN上方的點P滿足:45°≤∠MPN≤90°,則稱點P為線段MN的可視點.
)是平面直角坐標系xOy中的兩點,若平面內直線MN上方的點P滿足:45°≤∠MPN≤90°,則稱點P為線段MN的可視點.
(1)在點![]() ,
,![]() ,
,![]() ,A4(2,2)中,線段MN的可視點為 ;
,A4(2,2)中,線段MN的可視點為 ;
(2)若點B是直線y=x![]() 上線段MN的可視點,求點B的橫坐標t的取值范圍;
上線段MN的可視點,求點B的橫坐標t的取值范圍;
(3)直線y=x+b(b≠0)與x軸交于點C,與y軸交于點D,若線段CD上存在線段MN的可視點,直接寫出b的取值范圍.
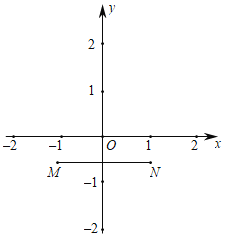
查看答案和解析>>
科目:初中數學 來源: 題型:
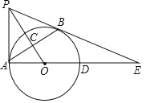
【題目】如圖,PA與⊙O相切于點A,過點A作AB⊥OP,垂足為C,交⊙O于點B.連接PB,AO,并延長AO交⊙O于點D,與PB的延長線交于點E.
(1)求證:PB是⊙O的切線;
(2)若OC=3,AC=4,求PB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
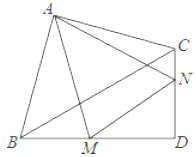
【題目】如圖,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分別在BD,CD上,∠MAN=45°,則△DMN的周長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
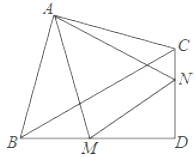
【題目】如圖,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=4,AB=AC,∠CBD=30°,M,N分別在BD,CD上,∠MAN=45°,則△DMN的周長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
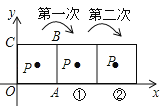
【題目】如圖,把正方形鐵片OABC置于平面直角坐標系中,頂點A的坐標為(3,0),點P(1,2)在正方形鐵片上,將正方形鐵片繞其右下角的頂點按順時針方向依次旋轉90°,第一次旋轉至圖①位置,第二次旋轉至圖②位置…,則正方形鐵片連續旋轉2017次后,點P的坐標為____________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
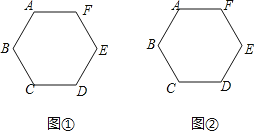
【題目】如圖,已知多邊形ABCDEF中,AB=AF,DC=DE,BC=EF,∠ABC=∠BCD.請僅用無刻度的直尺,分別按下列要求畫圖.
(1)在圖①中,畫出一個以BC為邊的矩形;
(2)在圖②中,若多邊形ABCDEF是正六邊形,試在AF上畫出點M,使得AM=![]() AF.
AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀以下材料,并解決相應問題:
材料一:換元法是數學中的重要方法,利用換元法可以從形式上簡化式子,在求解某些特殊方程時,利用換元法常常可以達到轉化的目的,例如在求解一元四次方程![]() ,就可以令
,就可以令![]() ,則原方程就被換元成
,則原方程就被換元成![]() ,解得 t 1,即
,解得 t 1,即![]() ,從而得到原方程的解是 x 1
,從而得到原方程的解是 x 1
材料二:楊輝三角形是中國數學上一個偉大成就,在中國南宋數學家楊輝 1261 年所著的《詳解九章算法》一書中出現,它呈現了某些特定系數在三角形中的一種有規律的幾何排列,下圖為楊輝三角形:

……………………………………
(1)利用換元法解方程:![]()
(2)在楊輝三角形中,按照自上而下、從左往右的順序觀察, an 表示第 n 行第 2 個數(其中 n≥4),bn 表示第 n 行第 3 個數,![]() 表示第
表示第![]() 行第 3 個數,請用換元法因式分解:
行第 3 個數,請用換元法因式分解:![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com