
【題目】費爾茲獎是國際上享有崇高榮譽的一個數學獎項,每4年評選一次,在國際數學家大會上頒給有卓越貢獻的年齡不超過40歲的年輕數學家,美籍華人丘成桐1982年獲得費爾茲獎.為了讓學生了解費爾茲獎得主的年齡情況,我們查取了截止到2018年60名費爾茲獎得主獲獎時的年齡數據,并對數據進行整理、描述和分析.下面給出了部分信息.
a.截止到2018年費爾茲獎得主獲獎時的年齡數據的頻數分布直方圖如圖1(數據分成5組,各組是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
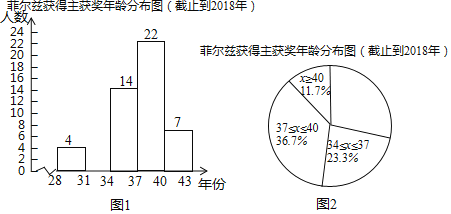
b.如圖2,在a的基礎上,畫出扇形統計圖;
c.截止到2018年費爾茲獎得主獲獎時的年齡在34≤x<37這一組的數據是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年時費爾茲獎得主獲獎時的年齡的平均數、中位數、眾數如下:
年份 | 平均數 | 中位數 | 眾數 |
截止到2018 | 35.58 | m | 37,38 |
根據以上信息,回答下列問題:
(1)依據題意,補全頻數直方圖;
(2)31≤x<34這組的圓心角度數是度,并補全扇形統計圖;
(3)統計表中中位數m的值是;
(4)根據以上統計圖表試描述費爾茲獎得主獲獎時的年齡分布特征.
【答案】(1)如圖見解析;(2)31≤x<34這組的圓心角度數是 78度,補全扇形統計圖見解析;(3)中位數m的值是 36;(4)答案不唯一,如:費爾茲獎得主獲獎時年齡集中在37歲至40歲.
【解析】
(1)根據總人數為60求出第二組的人數即可解決問題;
(2)根據圓心角=360°×百分比計算即可,根據百分比的和為1,求出第二組的百分比,即可畫出扇形統計圖;
(3)根據中位數的定義,中位數等于第30,31的年齡的平均數;
(4)答案不唯一,合理即可.
(1)如圖;
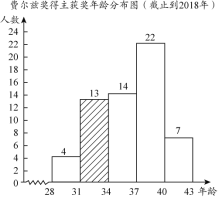
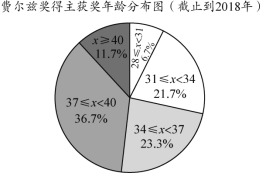
(2)31≤x<34這組的圓心角度數=360°×21.7%≈78°;
(3)中位數等于第30,31的年齡的平均數,第30,31的年齡位于34≤x<37組的最后2個,為36,36,故統計表中中位數m的值是 36;
(4)答案不唯一,如:費爾茲獎得主獲獎時年齡集中在37歲至40歲.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖,給出下列四個結論:①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),其中正確結論的個數是( )
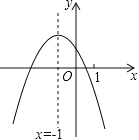
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B是反比例函數y=![]() (k≠0)圖象上的兩點,延長線段AB交y軸于點C,且點B為線段AC中點,過點A作AD⊥x軸于點D,點E為線段OD的三等分點,且OE<DE.連接AE、BE,若S△ABE=7,則k的值為( )
(k≠0)圖象上的兩點,延長線段AB交y軸于點C,且點B為線段AC中點,過點A作AD⊥x軸于點D,點E為線段OD的三等分點,且OE<DE.連接AE、BE,若S△ABE=7,則k的值為( )
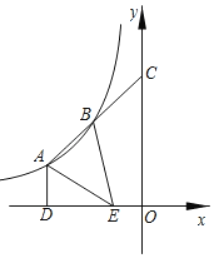
A.﹣12B.﹣10C.﹣9D.﹣6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,等腰直角△OAB的斜邊OB在x軸上,且OB=4,反比例函數y=![]() (x>0)的圖象經過OA的中點C,交AB于點D,則點D坐標是_____.
(x>0)的圖象經過OA的中點C,交AB于點D,則點D坐標是_____.
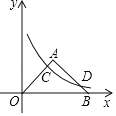
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三名快遞員某天的工作情況如圖所示,其中點![]() ,
,![]() ,
,![]() 的橫、縱坐標分別表示甲、乙、丙三名快遞員上午派送快遞所用的時間和件數;點
的橫、縱坐標分別表示甲、乙、丙三名快遞員上午派送快遞所用的時間和件數;點![]() ,
,![]() ,
,![]() ,的橫、縱坐標分別表示甲、乙、丙三名快遞員下午派送快遞所用的時間和件數.有如下三個結論:①上午派送快遞所用時間最短的是甲;②下午派送快遞件數最多的是丙;③在這一天中派送快遞總件數最多的是乙.上述結論中,所有正確結論的序號是( )
,的橫、縱坐標分別表示甲、乙、丙三名快遞員下午派送快遞所用的時間和件數.有如下三個結論:①上午派送快遞所用時間最短的是甲;②下午派送快遞件數最多的是丙;③在這一天中派送快遞總件數最多的是乙.上述結論中,所有正確結論的序號是( )
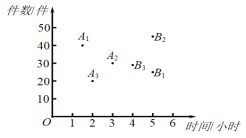
A. ①②B. ①③C. ②D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個三位數兩個數位上數字的和等于另一個數位上的數字,則稱這個三位數為“均衡三位數”.現從1,2,3,4,5這5個數字中任取三個數字,組成無重復數字且百位數字、十位數字、個位數字依次增大的三位數.
(1)請列舉出所有可能得到的三位數;
(2)小明和小亮玩一個游戲,游戲規則如下:若(1)中組成的三位數是“均衡三位數”,則小明勝;否則小亮勝.這個游戲公平嗎?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△ABC中,CAB=60°,點O為斜邊AB上一點,且OA=2,以OA為半徑的⊙O與BC相切于D,與AC交于點E,連接AD.
(1)求線段CD的長;
(2)求⊙O與Rt△ABC重疊部分的面積.(結果保留準確值)
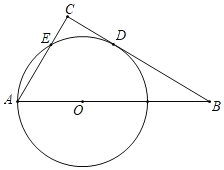
查看答案和解析>>
科目:初中數學 來源: 題型:
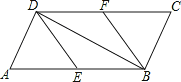
【題目】如圖,在平行四邊形ABCD中,E、F分別為邊AB、CD的中點,BD是對角線.
(1)求證:△ADE≌△CBF;
(2)若∠ADB是直角,則四邊形BEDF是什么四邊形?證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
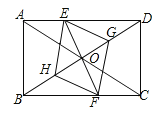
【題目】已知:如圖,在矩形ABCD中,點E在邊AD上,點F在邊BC上,且AE=CF,作EG∥FH,分別與對角線BD交于點G、H,連接EH,FG.
(1)求證:△BFH≌△DEG;
(2)連接DF,若BF=DF,則四邊形EGFH是什么特殊四邊形?證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com