
【題目】如圖,已知△ABC,點A在BC邊的上方,把△ABC繞點B逆時針方向旋轉(zhuǎn)60°得△DBE,繞點C順時針方向旋轉(zhuǎn)60°得△FEC,連接AD,AF.
(1)△ABD,△ACF,△BCE是什么特殊三角形?請說明理由;
(2)當(dāng)△ABC滿足什么條件時,四邊形ADEF是正方形?請說明理由;
(3)當(dāng)△ABC滿足什么條件時,以點A,D,E,F為頂點的四邊形不存在?請說明理由.
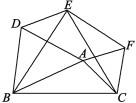
【答案】(1)△ABD,△ACF,△BCE都是等邊三角形,理由見解析;(2)當(dāng)∠BAC=150°,且AB=AC時,四邊形ADEF是正方形,理由見解析;(3)當(dāng)∠BAC=60°時,以點A,D,E,F為頂點的四邊形不存在,理由見解析.
【解析】
(1)△ABD、△ACF、△BCE都是等邊三角形;
(2)當(dāng)∠BAC=150°且AB=AC時,四邊形ADEF是正方形,理由為:由旋轉(zhuǎn)可知DE=AC,根據(jù)三角形ACF為等邊三角形,得到AC=AF,等量代換得到DE=AF,同理得到EF=AD,利用兩組對邊相等的四邊形為平行四邊形得到AFED為平行四邊形,若∠BAC=150°,利用周角定義求出∠DAF為直角,可得出平行四邊形AFED為矩形,再由AB=AC,三角形ADB與三角形ACF都是等邊三角形,得到AD=AF,矩形AFED為正方形,得證;
(3)當(dāng)∠BAC=60°時,以A、D、E、F為頂點的四邊形不存在,理由為:若∠BAC=60°,三角形ADB與三角形ACF都是等邊三角形,利用周角定義求出∠DAF為平角,即D、A、E、F四點共線,即以A、D、E、F為頂點的四邊形不存在.
(1)△ABD,△ACF,△BCE都是等邊三角形,
理由:由旋轉(zhuǎn)可知:AB=DB,∠ABD=60°,
AC=FC,∠ACF=60°;BC=BE,∠CBE=60°,
∴△ABD,△ACF,△BCE都是等邊三角形;
(2)當(dāng)∠BAC=150°,且AB=AC時,四邊形ADEF是正方形,
理由:∵△DBE是由△ABC繞點B旋轉(zhuǎn)60°而得到的,∴DE=AC,
由(1)知△ACF為等邊三角形,
∴AC=AF,∴DE=AF,
同理可得EF=AD,
∴四邊形ADEF是平行四邊形,
若∠BAC=150°,則∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-150°-60°-60°=90°,
∴四邊形ADEF是矩形,
又∵AB=AC,∴AD=AF,
則四邊形ADEF是正方形;
(3)當(dāng)∠BAC=60°時,以點A,D,E,F為頂點的四邊形不存在,
理由:若∠BAC=60°,則∠DAF=360°-∠BAC-∠DAB-∠FAC=360°-60°-60°-60°=180°,
此時,點A,D,E,F四點共線,
∴以點A,D,E,F為頂點的四邊形不存在.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數(shù)學(xué) 來源: 題型:
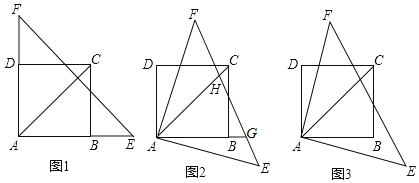
【題目】已知,如圖1,正方形ABCD的邊長為5,點E、F分別在邊AB、AD的延長線上,且BE=DF,連接EF.
(1)證明:EF⊥AC;
(2)將△AEF繞點A順時針方向旋轉(zhuǎn),當(dāng)旋轉(zhuǎn)角α滿足0°<α<45°時,設(shè)EF與射線AB交于點G,與AC交于點H,如圖所示,試判斷線段FH、HG、GE的數(shù)量關(guān)系,并說明理由.
(3)若將△AEF繞點A旋轉(zhuǎn)一周,連接DF、BE,并延長EB交直線DF于點P,連接PC,試說明點P的運動路徑并求線段PC的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,□ABCD中,BD是它的一條對角線,過A、C兩點作AE⊥BD,CF⊥BD,垂足分別為E、F,延長AE、CF分別交CD、AB于M、N。
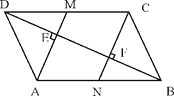
(1)求證:四邊形CMAN是平行四邊形。
(2)已知DE=4,F(xiàn)N=3,求BN的長。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
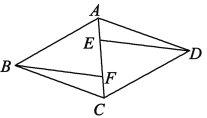
【題目】如圖,在菱形ABCD中,點E,F是對角線AC上的兩點,且AE=CF.
(1)圖中有哪幾對全等三角形,請一一列舉;
(2)求證:ED∥BF.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,某教學(xué)興趣小組想測量某建筑物的高度,他們在A點測得屋頂C的仰角為30°,然后沿AD方向前進10米,到達B點,在B點測得屋頂C的仰角為60°,已知測量儀AE的高度為1米,請你根據(jù)他們的測量數(shù)據(jù)計算建筑物CF的高度(結(jié)果保留根號).
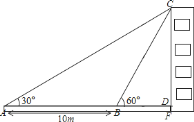
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,且
上,且![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() .
.

(1)求證:四邊形![]() 為矩形;
為矩形;
(2)判斷四邊形![]() 是什么特殊四邊形?并說明理由;
是什么特殊四邊形?并說明理由;
(3)求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某市舉行“行動起來,對抗霧霾”為主題的植樹活動,某街道積極響應(yīng),決定對該街道進行綠化改造,共購進甲、乙兩種樹共50棵,已知甲樹每棵800元,乙樹每棵1200元.
(1)若購買兩種樹的總金額為56000元,求甲、乙兩種樹各購買了多少棵?
(2)若購買甲樹的金額不少于購買乙樹的金額,至少應(yīng)購買甲樹多少棵?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com