
【題目】某校為了了解本校七年級學生的視力情況(視力情況分為:不近視,輕度近視,中度近視,重度近視),隨機對七年級的部分學生進行了抽樣調查,將調查結果進行整理后,繪制了如下不完整的統計圖,其中中度近視人數是不近視與重度近視人數之和的一半.
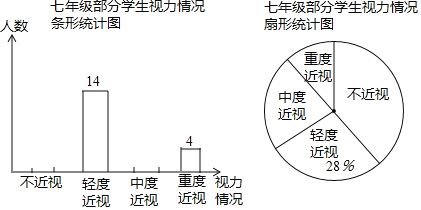
請你根據以上信息解答下列問題:
(1)求本次調查的學生人數;
(2)補全條形統計圖.在扇形統計圖中,求“中度近視”對應扇形的圓心角的度數;
(3)若該校七年級學生有1200人,請你估計該校七年級近視(包括輕度近視,中度近視,重度近視)的學生大約有多少人?
【答案】(1)50(人);(2)圖見解析,86.4°;(3)720
【解析】
(1)根據輕度近視的人數是14人,占總人數的28%,即可求得總人數;
(2)設中度近視的人數是x人,則不近視與重度近視人數的和為2x,列方程求得x的值,即可求得不近視的人數,然后利用360°乘以對應的百分比即可求得圓心角的度數;
(3)利用總人數乘以對應的百分比即可求解.
解:(1)本次調查的學生人數為14÷28%=50(人);
(2)設中度近視的人數是x人,則不近視與重度近視人數的和為2x,則x+2x+14=50,
解得:x=12,
則中度近視的人數是12,不近視的人數是:24﹣4=20(人),
所以“中度近視”對應扇形的圓心角度數是:360°×![]() =86.4°;
=86.4°;
補全條形圖如下:
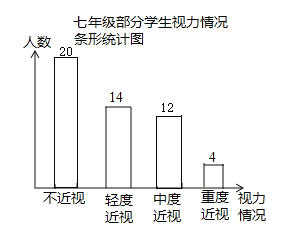
(3)估計該校七年級近視(包括輕度近視,中度近視,重度近視)的學生大約有
1200×![]() =720(人).
=720(人).


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD(AB<AD)沿BD折疊后,點C落在點E處,且BE交AD于點F,若AB=4,BC=8.

(1)求DF的長;
(2)求△DBF和△DEF的面積;
(3)求△DBF中F點到BD邊上的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳2022年北京﹣張家口冬季奧運會,小王在網上銷售一種成本為20元/件的本屆冬季奧運會宣傳文化衫,銷售過程中的其他各種費用(不再含文化衫成本)總計50(百元),有關銷售量y(百件)與銷售價格x(元/件)的相關信息如下:
銷售量y(百件) | y=﹣0.1x+8 | y= |
銷售價格x(元/件) | 30≤x≤60 | 60<x≤80 |
(1)求銷售這種文化衫的純利潤w(百元)與銷售價格x(元/件)的函數關系式;
(2)銷售價格定為多少元/件時,獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
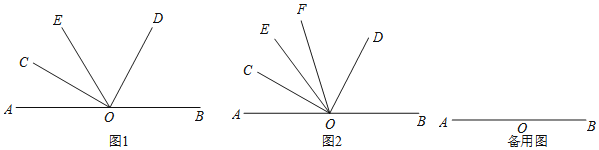
【題目】點O為直線AB上一點,在直線AB上側任作一個∠COD,使得∠COD=90°.
(1)如圖1,過點O作射線OE,當OE恰好為∠AOD的角平分線時,請直接寫出∠BOD與∠COE之間的倍數關系,即∠BOD= ______ ∠COE(填一個數字);
(2)如圖2,過點O作射線OE,當OC恰好為∠AOE的角平分線時,另作射線OF,使得OF平分∠COD,求∠FOB+∠EOC的度數;
(3)在(2)的條件下,若∠EOC=3∠EOF,求∠AOE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分) 2011年5月上旬,無錫市共有35000余名學生參加中考體育測試,為了了解九年級男生立定跳遠的成績,從某校隨機抽取了50名男生的測試成績,根
據測試評分標準,將他們的得分按優秀、良好、及格、不及格(分別用A、B、C、D
表示)四個等級進行統計,并繪制成如圖所示的扇形圖和統計表:
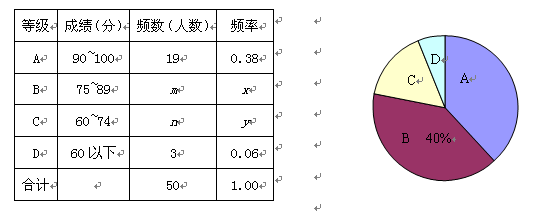
請你根據以上圖表提供的信息,解答下列問題:
【1】(1) m= ,n= ,x= ,y= ;
【2】(2)在扇形圖中,C等級所對應的圓心角是 度;
【3】(3)如果該校九年級共有500名男生參加了立定跳遠測試,那么請你估計這些男生成績等級達到優秀和良好的共有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了美化環境,建設宜居成都,我市準備在一個廣場上種植甲、乙兩種花卉.經市場調查,甲種花卉的種植費用![]() (元)與種植面積
(元)與種植面積![]() 之間的函數關系如圖所示,乙種花卉的種植費用為每平方米100元.
之間的函數關系如圖所示,乙種花卉的種植費用為每平方米100元.

(1)直接寫出當![]() 和
和![]() 時,
時,![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)廣場上甲、乙兩種花卉的種植面積共![]() ,若甲種花卉的種植面積不少于
,若甲種花卉的種植面積不少于![]() ,且不超過乙種花卉種植面積的2倍,那么應該怎樣分配甲、乙兩種花卉的種植面積才能使種植費用最少?最少總費用為多少元?
,且不超過乙種花卉種植面積的2倍,那么應該怎樣分配甲、乙兩種花卉的種植面積才能使種植費用最少?最少總費用為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】|a|+|b|=|a+b|,則a,b關系是( )
A. a,b的絕對值相等
B. a,b異號
C. a+b的和是非負數
D. a、b同號或a、b其中一個為0
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題背景
如圖①,BC是⊙O的直徑,點A在⊙O上,AB=AC,P為![]() 上一動點(不與B,C重合),
上一動點(不與B,C重合),
求證:![]() PA=PB+PC.
PA=PB+PC.

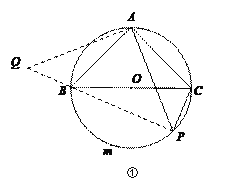
請你根據小明同學的思考過程完成證明過程.
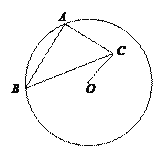
(2)類比遷移
如圖②,⊙O的半徑為3,點A,B在⊙O上,C為⊙O內一點,AB=AC,AB⊥AC,垂足為A,求OC的最小值.

(3)拓展延伸
如圖,⊙O的半徑為3,點A,B在⊙O上,C為⊙O內一點,AB=![]() AC,AB⊥AC,垂足為A,則OC的最小值為 .
AC,AB⊥AC,垂足為A,則OC的最小值為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com