
【題目】計算:
(1)![]()
(2)小明解不等式![]() ≤1的過程如下,請指出他解答過程中開始出現錯誤步驟的序號,并寫出正確的解答過程.
≤1的過程如下,請指出他解答過程中開始出現錯誤步驟的序號,并寫出正確的解答過程.
解:去分母得:3(1+x)﹣2(2x+1)≤1……①
去括號得:3+3x﹣4x+1≤1……②
移項得:3x﹣4x≤1﹣3﹣1……③
合并同類項得:﹣x≤﹣3……④
兩邊都除以﹣1得:x≤3……⑤
解:開始出現錯誤的步驟序號為 ,正確的解答過程 .
(3)已知實數x,y滿足方程組![]() ,求
,求![]() 的平方根;
的平方根;
(4)求不等式組 的整數解.
的整數解.
【答案】(1)1+![]() ;(2)①,見解析;(3)±2;(4)-2,-1
;(2)①,見解析;(3)±2;(4)-2,-1
【解析】
(1)根據立方根和絕對值的性質計算即可
(2)根據一元一次不等式的解法,找出錯誤的步驟,并寫出正確的解答過程即可.
(3)先求出方程組的解,再求出4x2y的值,再求出平方根即可.
(4)先求出不等式組的解集,再找出整數解即可
(1)原式=5-3+![]() -1=1+
-1=1+![]()
(2)開始出現錯誤的步驟序號為①,正確解答過程如下:
去分母,得3(1+x)2(2x+1)6,
去括號,得3+3x4x26,
移項,得3x4x63+2,
合并同類項,得x5,
兩邊都除以1,得x5.
(3)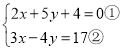
①×4+②×5得:23x=69,
解得:x=3,
把x=3代入②得:94y=17,
解得:y=2,
∴4x2y=4×32×(2)=16,![]() =4
=4
所以![]() 的平方根是±2.
的平方根是±2.
(4)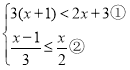 ,
,
由不等式①得x<0,
由不等式②得x≥-2,
所以不等組的解集為-2≤x<0,
則這個不等式組的整數解是-2,-1.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:
【題目】將兩塊全等的含![]() 角的直角三角板按圖
角的直角三角板按圖![]() 的方式放置,已知
的方式放置,已知![]() ,
,![]() .
.
![]() 固定三角板
固定三角板![]() ,然后將三角板
,然后將三角板![]() 繞點
繞點![]() 順時針方向旋轉至圖
順時針方向旋轉至圖![]() 所示的位置,
所示的位置,![]() 與
與![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() ,
,![]() 與
與![]() 交于點
交于點![]() .
.
①填空:當旋轉角等于![]() 時,
時,![]() ________度;
________度;
②當旋轉角等于多少度時,![]() 與
與![]() 垂直?請說明理由.
垂直?請說明理由.
![]() 將圖
將圖![]() 中的三角板
中的三角板![]() 繞點
繞點![]() 順時針方向旋轉至圖
順時針方向旋轉至圖![]() 所示的位置,使
所示的位置,使![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,試說明
,試說明![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
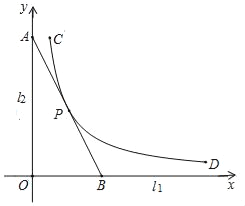
【題目】如圖,直線l1,l2是緊靠某湖泊的兩條相互垂直的公路,曲線段CD是該湖泊環湖觀光大道的一部分.現準備修建一條直線型公路AB,用以連接兩條公路和環湖觀光大道,且直線AB與曲線段CD有且僅有一個公共點P.已知點C到l1,l2的距離分別為8km和1km,點P到l1的距離為4km,點D到l1的距離為0.8km.若分別以l1,l2為x軸、y軸建立平面直角坐標系xOy,則曲線段CD對應的函數解析式為y=![]() .
.
(1)求k的值,并指出函數y=![]() 的自變量的取值范圍;
的自變量的取值范圍;
(2)求直線AB的解析式,并求出公路AB長度(結果保留根號).
查看答案和解析>>
科目:初中數學 來源: 題型:
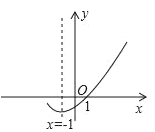
【題目】如圖,是二次函數y=ax2+bx+c(a≠0)的圖象的一部分,給出下列命題:
①abc<0;②b>2a;③a+b+c=0;④8a+c>0;⑤ax2+bx+c=0的兩根分別為﹣3和1.
其中正確的命題有( )
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的正方形網格中,每個小正方形的邊長均為1個單位, ![]() 的三個頂點都在格點上.
的三個頂點都在格點上.
(1)在網格中畫出![]() 向下平移3個單位得到的
向下平移3個單位得到的![]() ;
;
(2)在網格中畫出![]() 關于直線
關于直線![]() 對稱的
對稱的![]() ;
;
(3)在直線![]() 上畫一點
上畫一點![]() ,使得
,使得![]() 的值最大.
的值最大.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把自然數按如圖的次序排列在直角坐標系中,每個點坐標就對應著一個自然數,例如點(0,0)對應的自然數是1,點(1,2)對應的自然數是14,那么點(1,4)對應的自然數是____;點(n,n)對應的自然數是____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了測量被池塘隔開的A,B兩點之間的距離,根據實際情況,作出如圖所示的圖形,其中AB⊥BE,EF⊥BE,AF交BE于點D,C在BD上.有四位同學分別測量出以下4組數據:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根據所測數據,求出A,B兩點之間距離的有( )
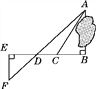
A. 1組 B. 2組 C. 3組 D. 4組
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.動點P、Q分別從點A、B同時開始移動,點P的速度為1 cm/秒,點Q的速度為2 cm/秒,點Q移動到點C后停止,點P也隨之停止運動下列時間瞬間中,能使△PBQ的面積為15cm 的是( )
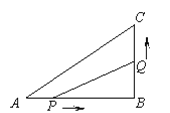
A. 2秒鐘 B. 3秒鐘 C. 4秒鐘 D. 5秒鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
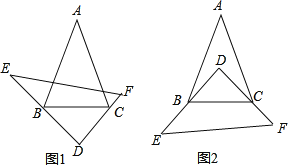
【題目】已知:在△ABC和△DEF中,∠A=40°,∠E+∠F=100°,將△DEF如圖擺放,使得∠D的兩條邊分別經過點B和點C.
(1)當將△DEF如圖1擺放時,則∠ABD+∠ACD= 度;
(2)當將△DEF如圖2擺放時,請求出∠ABD+∠ACD的度數,并說明理由.
(3)能否將△DE擺放到某個位置時,使得BD、CD同時平分∠ABC和∠ACB?直接寫出結論 (填“能”或“不能”)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com