
【題目】如圖,在一張三角形紙片ABC中,AB=10cm,BC=7cm,AC=6cm,沿過點B的直線折疊這個三角形,使頂點C落在邊AB上的點E處,折痕為BD.

(1)求△AED的周長.
(2)說明BD垂直平分EC.
科目:初中數學 來源: 題型:
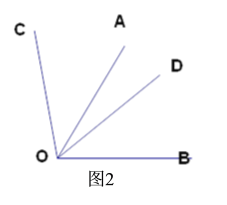
【題目】(1)如圖 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代數式表示∠BOC.

(2)如圖2,若∠AOB=∠COD=60°,直接寫出∠AOC與∠BOD的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,二次函數y=x2+bx+c(b,c都是常數)的圖象經過點(1,0)和(0,2).
(1)當﹣2≤x≤2時,求y的取值范圍.
(2)已知點P(m,n)在該函數的圖象上,且m+n=1,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“十一”黃金周期間,重慶仙女山風景區7天假期中每天旅游的人數變化如下表(正數表示比前一天多的人數,負數表示比前一天少的人數):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人數變化 單位:萬人 | +1.2 | +0.4 | +0.8 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
(1)若9月30日的游客人數記為a,請用含a的式子表示10月5日的游客人數: 萬人.
(2)判斷七天內游客人數最多的是 日,最少的是 日.
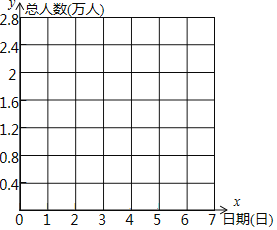
(3)以9月30日的游客人數為0點,用折線統計圖表示這7天的游客人數情況:人數變化(萬人)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:數和形是數學的兩個主要研究對象,我們經常運用數形結合,樹形轉化的方法解決一些數學問題,小明在求同一坐標軸上兩點間的距離時發現,對于平面直角坐標系內任意兩點P1(x1,y1),P2(x2,y2),可通過構造直角三角形利用圖1得到結論:P1P2=![]() ,他還利用圖2證明了線段P1P2的中點P(x,y),P的坐標公式:x=
,他還利用圖2證明了線段P1P2的中點P(x,y),P的坐標公式:x=![]() ,y=
,y=![]() .
.
啟發應用:
如圖3:在平面直角坐標系中,已知A(8,0),B(0,6),C(1,7),⊙M經過原點O及點A,B,
(1)求⊙M的半徑及圓心M的坐標;
(2)判斷點C與⊙M的位置關系,并說明理由;
(3)若∠BOA的平分線交AB于點N,交⊙M于點E,分別求出OE的表達式y1,過點M的反比例函數的表達式y2,并根據圖象,當y2>y1>0時,請直接寫出x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:
![]() “明天降雨的概率是
“明天降雨的概率是![]() ”表示明天有半天都在降雨;
”表示明天有半天都在降雨;
![]() 無理數是開方開不盡的數;
無理數是開方開不盡的數;
![]() 若
若![]() 為實數,則
為實數,則![]() 是不可能事件;
是不可能事件;
![]() 的平方根是
的平方根是![]() ,用式子表示是
,用式子表示是![]() ;
;
![]() 某班的5位同學在向“創建圖書角”捐款活動中,捐款數如下(單位:元):8,3,8,2,4,那么這組數據的眾數是8,中位數是4,平均數是5.其中正確的個數有( )
某班的5位同學在向“創建圖書角”捐款活動中,捐款數如下(單位:元):8,3,8,2,4,那么這組數據的眾數是8,中位數是4,平均數是5.其中正確的個數有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片 ABCD,使AD落在BD上,點A恰好與BD上的點F重合.展開后,折痕DE分別交AB、 AC于點E、G.連接GF.則下列結論錯誤的是( )
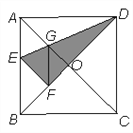
A. ∠AGD=112.5° B. 四邊形AEFG是菱形 C. tan∠AED=2 D. BE=2OG
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線 y1 與 y2 相交于點C , y1 與 x 軸交于點 D ,與 y 軸交于點0,1, y2 與 x 軸 交于點 B3,0,與 y 軸交于點 A ,下列說法正確的個數有( )
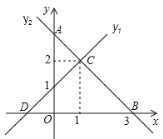
①y1的 解 析 式 為![]() ;② OA OB ;③
;② OA OB ;③![]() ;④
;④![]() ;⑤ AOB BCD .
;⑤ AOB BCD .
A.2 個B.3個C.4 個D.5 個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com