
【題目】如圖,在平行四邊形ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B、F為圓心,大于 ![]() BF長為半徑畫弧,兩弧交于一點P,連
BF長為半徑畫弧,兩弧交于一點P,連
接AP并延長交BC于點E,連接EF.
(1)四邊形ABEF是;(選填矩形、菱形、正方形、無法確定)(直接填寫結果)
(2)AE,BF相交于點O,若四邊形ABEF的周長為40,BF=10,則AE的長為 , ∠ABC=°.(直接填寫結果)
【答案】
(1)菱形
(2)10 ![]() ;120
;120
【解析】解:(1)在△AEB和△AEF中, ,
,
∴△AEB≌△AEF,
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四邊形ABEF是平行四邊形
∵AB=AF,
∴四邊形ABEF是菱形.
所以答案是菱形.
2)∵四邊形ABEF是菱形,
∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,
∵AB=10,
∴AB=2BO,∵∠AOB=90°
∴∠BA0=30°,∠ABO=60°,
∴AO= ![]() BO=5
BO=5 ![]() ,∠ABC=2∠ABO=120°.
,∠ABC=2∠ABO=120°.
所以答案是10 ![]() ,120.
,120.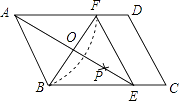
【考點精析】解答此題的關鍵在于理解平行四邊形的性質的相關知識,掌握平行四邊形的對邊相等且平行;平行四邊形的對角相等,鄰角互補;平行四邊形的對角線互相平分.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=ax2+bx+c與x軸相交于A、B兩點,與y軸相交于點C(0,3).且點A的坐標為(﹣1,0),點B的坐標為(3,0),點P是拋物線上第一象限內的一個點. 
(1)求拋物線的函數表達式;
(2)連PO、PB,如果把△POB沿OB翻轉,所得四邊形POP′B恰為菱形,那么在拋物線的對稱軸上是否存在點Q,使△QAB與△POB相似?若存在求出點Q的坐標;若不存在,說明理由;
(3)若(2)中點Q存在,指出△QAB與△POB是否位似?若位似,請直接寫出其位似中心的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
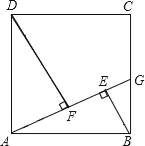
【題目】如圖,在邊長為4的正方形ABCD中,點G是BC邊上的任意一點(不同于端點B、C),連接AG,過B、D兩點作BE⊥AG,DF⊥AG,垂足分為E、F.
(1)求證:△ABE≌△DAF;
(2)若△ADF的面積為1,試求|BE﹣DF|的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,一次函數y=kx+3的圖象經過點A(1,4).
(1)求這個一次函數的解析式;
(2)試判斷點B(-1,5),C(0,3),D(2,1)是否在這個一次函數的圖象上.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在平面直角坐標系中,O是坐標原點,點A(2,5)在反比例函數y= ![]() 的圖象上.一次函數y=x+b的圖象過點A,且與反比例函數圖象的另一交點為B.
的圖象上.一次函數y=x+b的圖象過點A,且與反比例函數圖象的另一交點為B.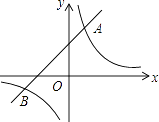
(1)求k和b的值;
(2)設反比例函數值為y1 , 一次函數值為y2 , 求y1>y2時x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=6,BC=4,過對角線BD中點O的直線分別交AB,CD邊于點E,F.
(1)求證:四邊形BEDF是平行四邊形;
(2)當四邊形BEDF是菱形時,求EF的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com