
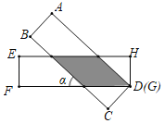
【題目】如圖,有兩張矩形紙片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.把紙片ABCD交叉疊放在紙片EFGH上,使重疊部分為平行四邊形,且點D與點G重合.當(dāng)兩張紙片交叉所成的角α最小時,sinα等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由“ASA”可證△CDM≌△HDN,可證MD=DN,即可證四邊形DNKM是菱形,當(dāng)點B與點E重合時,兩張紙片交叉所成的角a最小,可求DM=![]() ,即可求
,即可求![]() 的值.
的值.
解:如圖,
∵∠ADC=∠HDF=90°
∴∠CDM=∠NDH,且CD=DH,∠H=∠C=90°
∴△CDM≌△HDN(ASA)
∴MD=ND,且四邊形DNKM是平行四邊形
∴四邊形DNKM是菱形
∴KM=DM
∵sinα=sin∠DMC=![]() ,
,
∴當(dāng)點B與點E重合時,兩張紙片交叉所成的角a最小,
設(shè)MD=a=BM,則CM=8-a,
∵MD2=CD2+MC2,
∴a2=4+(8-a)2,
∴a=![]() ,
,
∴DM=![]() ,
,
∴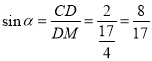 ;
;
故選:B.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案科目:初中數(shù)學(xué) 來源: 題型:
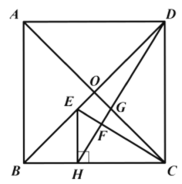
【題目】如圖,在邊長為1的正方形![]() 中,對角線
中,對角線![]() ,
,![]() 相交于O.點.H為邊
相交于O.點.H為邊![]() 上的點,過點H作
上的點,過點H作![]() ,交線段
,交線段![]() 于點E,連接
于點E,連接![]() 交
交![]() 于點F,交
于點F,交![]() 于點G.若
于點G.若![]() ,則
,則![]() 的長為__________.
的長為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
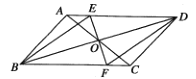
【題目】如圖,在平行四邊形![]() 中,
中,![]() 、
、![]() 相交于點
相交于點![]() ,
,![]() 交
交![]() 邊于點
邊于點![]() ,連接
,連接![]() .
.
(1)如圖,求證:![]() 平分
平分![]() ;
;
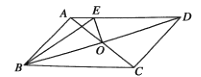
(2)如圖,延長![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,在不添加任何輔助線的條件下,請直接寫出面積為
,在不添加任何輔助線的條件下,請直接寫出面積為![]() 面積2倍的三角形.
面積2倍的三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】把![]() 個只有顏色不同的小球分別裝入甲乙丙三個布袋里其中甲布袋里有
個只有顏色不同的小球分別裝入甲乙丙三個布袋里其中甲布袋里有![]() 個紅球,
個紅球,![]() 個白球;乙布袋里有
個白球;乙布袋里有![]() 個紅球,
個紅球,![]() 個白球;丙布袋里有
個白球;丙布袋里有![]() 個紅球,
個紅球,![]() 個白球.
個白球.
![]() 求
求![]() 的值,并求從甲、乙兩個布袋中隨機各摸出
的值,并求從甲、乙兩個布袋中隨機各摸出![]() 個小球,求摸出的兩個小球都是紅球的概率;
個小球,求摸出的兩個小球都是紅球的概率;
![]() 利用列表或樹狀圖法求從甲、乙、丙三個布袋中隨機各摸出
利用列表或樹狀圖法求從甲、乙、丙三個布袋中隨機各摸出![]() 個小球,求摸出的三個小球是一紅二白的概率.
個小球,求摸出的三個小球是一紅二白的概率.
![]() 將丙袋子中原有的所有小球拿出,另裝
將丙袋子中原有的所有小球拿出,另裝![]() 個只有顏色不同的球,其中
個只有顏色不同的球,其中![]() 個白球,
個白球,![]() 個紅球,若從袋中取出若千個紅球,換成相同數(shù)量的黃球.?dāng)嚢杈鶆蚝螅沟秒S機從袋中摸出兩個球,顏色是一白一黃的概率為
個紅球,若從袋中取出若千個紅球,換成相同數(shù)量的黃球.?dāng)嚢杈鶆蚝螅沟秒S機從袋中摸出兩個球,顏色是一白一黃的概率為![]() ,(不放回拿球)求袋中有幾個紅球被換成了黃球?
,(不放回拿球)求袋中有幾個紅球被換成了黃球?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“低碳生活,綠色出行”,2017年1月,某公司向深圳市場新投放共享單車640輛.
(1)若1月份到4月份新投放單車數(shù)量的月平均增長率相同,3月份新投放共享單車1000輛.請問該公司4月份在深圳市新投放共享單車多少輛?
(2)考慮到自行車市場需求不斷增加,某商城準(zhǔn)備用不超過70000元的資金再購進A,B兩種規(guī)格的自行車100輛,已知A型的進價為500元/輛,售價為700元/輛,B型車進價為1000元/輛,售價為1300元/輛。假設(shè)所進車輛全部售完,為了使利潤最大,該商城應(yīng)如何進貨?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的一元二次方程![]() .
.
(1)若方程有兩個不相等的實數(shù)根,求k的取值范圍;
(2)當(dāng)k取滿足(1)中條件的最小整數(shù)時,設(shè)方程的兩根為α和β,求代數(shù)式![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校舉辦初中生數(shù)學(xué)素養(yǎng)大賽,比賽共設(shè)四個項目:七巧拼圖、趣題巧解、數(shù)學(xué)應(yīng)用和魔方復(fù)原,每個項目得分都按一定百分比折算后記入總分,并規(guī)定總分在85分以上(含85分)設(shè)為一等獎.下表為甲、乙、丙三位同學(xué)的得分情況(單位:分),其中甲的部分信息不小心被涂黑了.
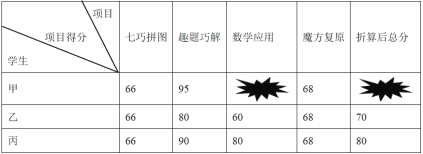
據(jù)悉,甲、乙、丙三位同學(xué)的七巧拼圖和魔方復(fù)原兩項得分折算后的分?jǐn)?shù)之和均為20分.設(shè)趣題巧解和數(shù)學(xué)應(yīng)用兩個項目的折算百分比分別為x和y,請用含x和y的二元一次方程表示乙同學(xué)“趣題巧解和數(shù)學(xué)應(yīng)用”兩項得分折算后的分?jǐn)?shù)之和為_________________;如果甲獲得了大賽一等獎,那么甲的“數(shù)學(xué)應(yīng)用”項目至少獲得_________分.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,E,F是正方形ABCD的對角線AC上的兩點,AE=CF,連接DE、BE、BF、DF.
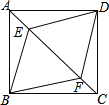
(1)求證:四邊形BEDF為菱形;
(2)若菱形BEDF的邊長為2![]() ,AE=2,求正方形ABCD的邊長.
,AE=2,求正方形ABCD的邊長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】近幾年購物的支付方式日益增多,某數(shù)學(xué)興趣小組就此進行了抽樣調(diào)查.調(diào)查結(jié)果顯示,支付方式有:A微信、B支付寶、C現(xiàn)金、D其他,該小組對某超市一天內(nèi)購買者的支付方式進行調(diào)查統(tǒng)計,得到如下兩幅不完整的統(tǒng)計圖.

請你根據(jù)統(tǒng)計圖提供的信息,解答下列問題:
(1)本次一共調(diào)查了多少名購買者?
(2)請補全條形統(tǒng)計圖;在扇形統(tǒng)計圖中A種支付方式所對應(yīng)的圓心角為 度.
(3)若該超市這一周內(nèi)有1600名購買者,請你估計使用A和B兩種支付方式的購買者共有多少名?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com