
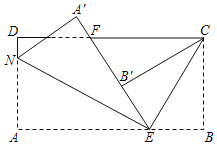
【題目】如圖,長方形紙片ABCD,點E、F分別在邊AB、CD上,連接EF.將∠BEF對折,點B落在直線EF上的點B′處,得到折痕EC;將∠AEF對折,點A落在直線EF上的點A′處,得到折痕EN.
(1)若∠BEB′=110°,則∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.
(2)若∠BEB′=m°,則(1)中∠BEC+∠AEN的值是否改變?請說明你的理由.
(3)將∠ECF對折,點E剛好落在F處,且折痕與B′C重合,求∠AEN的度數.(提示,長方形的四個角都是90°)
【答案】(1)55,35,90;(2)不改變,理由見解析;(3)∠AEN=30°
【解析】
(1)由對折的定義∠BEC=∠B'EC=![]() ∠BEB'=55°,∠AEN=∠A'EN=
∠BEB'=55°,∠AEN=∠A'EN=![]() ∠AEA'=
∠AEA'=![]() (180°﹣110°)=35°,得出∠BEC+∠AEN=90°即可;
(180°﹣110°)=35°,得出∠BEC+∠AEN=90°即可;
(2)同(1)得出∠BEC=∠B'EC=![]() ∠BEB',∠AEN=∠A'EN=
∠BEB',∠AEN=∠A'EN=![]() ∠AEA',得出∠BEC+∠AEN=
∠AEA',得出∠BEC+∠AEN=![]() ∠BEB'+
∠BEB'+![]() (180°﹣∠BEB')=90°;
(180°﹣∠BEB')=90°;
(3)由長方形的定義得出∠BCE+∠ECB′+∠B′CF=90°,由對折得出∠BCE=∠ECB′=∠B′CF=30°,求出∠FCE=60°,由平行線的性質得出∠BEC=∠FCE=60°,由(2)得出∠BEC+∠AEN=90°,即可得出答案.
解:(1)∵將∠BEF對折,點B落在直線EF上的點B′處,得到折痕EC;將∠AEF對折,點A落在直線EF上的點A′處,得到折痕EN.
∴∠BEC=∠B'EC=![]() ∠BEB'=55°,∠AEN=∠A'EN=
∠BEB'=55°,∠AEN=∠A'EN=![]() ∠AEA'=
∠AEA'=![]() (180°﹣110°)=35°,
(180°﹣110°)=35°,
∴∠BEC+∠AEN=90°,
故答案為:55,35,90;
(2)若∠BEB′=m°,則(1)中∠BEC+∠AEN的值不改變,理由如下:
同(1)得:∠BEC=∠B'EC=![]() ∠BEB',∠AEN=∠A'EN=
∠BEB',∠AEN=∠A'EN=![]() ∠AEA',
∠AEA',
∴∠BEC+∠AEN=![]() ∠BEB'+
∠BEB'+![]() (180°﹣∠BEB')=90°;
(180°﹣∠BEB')=90°;
(3)∵長方形紙片ABCD,
∴AB∥CD,∠BCD=90°,
∴∠BCE+∠ECB′+∠B′CF=90°,
∵將∠ECF對折,點E剛好落在F處,且折痕與B′C重合,
∴∠BCE=∠ECB′=∠B′CF=30°,
∴∠FCE=60°,
∵AB∥CD,
∴∠BEC=∠FCE=60°,
由(2)得:∠BEC+∠AEN=90°,
∴∠AEN=90°﹣∠BEC=90°﹣60°=30°.


 陽光課堂課時作業(yè)系列答案
陽光課堂課時作業(yè)系列答案科目:初中數學 來源: 題型:
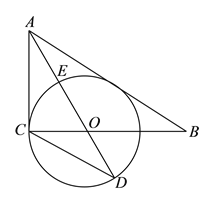
【題目】如圖,在![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的角平分線,以
的角平分線,以![]() 為圓心,
為圓心, ![]() 為半徑作⊙
為半徑作⊙![]() .
.
(![]() )求證:
)求證: ![]() 是⊙
是⊙![]() 的切線.
的切線.
(![]() )已知
)已知![]() 交⊙
交⊙![]() 于點
于點![]() ,延長
,延長![]() 交⊙
交⊙![]() 于點
于點![]() ,
, ![]() ,求
,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的條件下,設⊙
)的條件下,設⊙![]() 的半徑為
的半徑為![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將一張長方形的紙對折(使寬邊重合,然后再對折),第一次對折,得到一條折痕連同長方形的兩條寬邊共3條等寬線(如圖(1),第二次對折(每次的折痕與上次的折痕保持平行),得到5條等寬線(如圖(2)所示),連續(xù)對折三次后,可以得到9條等寬線(如圖(3所示),對折四次可以得到17條等寬線,如果對折6次,那么可以得到的等寬線條數是______條.

查看答案和解析>>
科目:初中數學 來源: 題型:
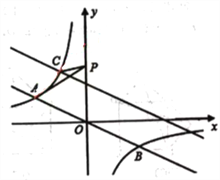
【題目】如圖,直角坐標系中,直線![]() 與反比例函數
與反比例函數![]() 的圖象交于A,B兩點,已知A點的縱坐標是2.
的圖象交于A,B兩點,已知A點的縱坐標是2.
(1)求反比例函數的解析式.
(2)將直線![]() 沿x軸向右平移6個單位后,與反比例函數在第二象限內交于點C.動點P在y軸正半軸上運動,當線段PA與線段PC之差達到最大時,求點P的坐標.
沿x軸向右平移6個單位后,與反比例函數在第二象限內交于點C.動點P在y軸正半軸上運動,當線段PA與線段PC之差達到最大時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
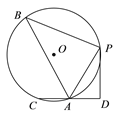
【題目】如圖,在⊙O中,B,P,A,C是圓上的點,PB= PC, PD⊥CD,CD交⊙O于A,若AC=AD,PD =![]() ,sin∠PAD =
,sin∠PAD =![]() ,則△PAB的面積為_______.
,則△PAB的面積為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在△ABC中,∠A=90°.
(1)請用圓規(guī)和直尺作出⊙P,使圓心P在AC邊上,且與AB,BC兩邊都相切(保留作圖痕跡,不寫作法和證明);

(2)在(1)的條件下,若∠B=45°,AB=1,⊙P切BC于點D,求劣弧![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
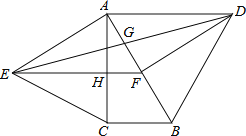
【題目】如圖,分別以直角△ABC的斜邊AB,直角邊AC為邊向△ABC外作等邊△ABD和等邊△ACE,F為AB的中點,DE與AB交于點G,EF與AC交于點H,∠ACB=90°,∠BAC=30°.給出如下結論:
①EF⊥AC;②四邊形ADFE為菱形;③AD=4AG;④FH=![]() BD
BD
其中正確結論的為______(請將所有正確的序號都填上).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在求兩位數的平方時,可以用“列豎式”的方法進行速算,求解過程如圖1所示.仿照圖1,用“列豎式”的方法計算一個兩位數的平方,部分過程如圖2所示,若這個兩位數的個位數字為a,則這個兩位數為( )
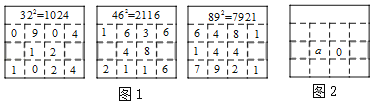
A.a﹣50B.a+50C.a﹣20D.a+20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(大豐某校數學興趣小組活動場景)
(課堂再現)
師:同學們還記得教材P43分配律a(b+c)=ab+ac嗎?現在,老師和大家一起來用幾何的方法來證明這個公式。相信今天會驚喜不斷。(學生期待驚喜中………),
(教者呈現教具)老師手上有兩個長方形,長分別是b、c,寬都是a,(如圖1)它們各自面積是多少?
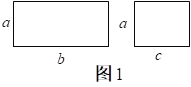

生1:面積分別為ab、ac。
師:現在我們把它們拼在一起(如圖2),組成了一個新長方形,新長方形面積又是多少呢?
生2:![]()
師:所以……
生3:所以得到![]() ,也就是說
,也就是說![]() (真好玩!)
(真好玩!)
師:相信大家能用類似方法來推導一個我們暫時還沒學習的公式,老師期待大家給我的驚喜哦!(屏幕上呈現問題)
(拓展延伸)
將邊長為a的正方形紙板上剪去一個邊長為b的正方形(如圖3),將剩余的紙板沿虛線剪開,拼成如圖4的梯形。

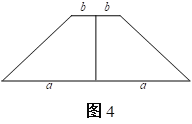
(1)你能得到一個什么等式.(用含a、b的式子表示)
(再接再厲)
(2)直接運用上面你發(fā)現的公式完成運算:![]()
(拓展提高)
(3)直接運用上面你發(fā)現的公式解下列方程:![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com