
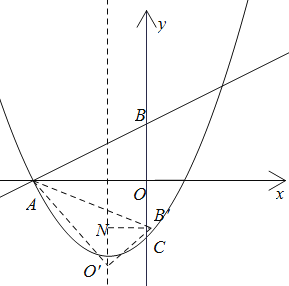
【題目】如圖,直線![]() 交
交![]() 軸于點A,交
軸于點A,交![]() 軸于點B,拋物線
軸于點B,拋物線![]() 經(jīng)過點A,交
經(jīng)過點A,交![]() 軸于點
軸于點![]() ,點P為直線AB下方拋物線上一動點,過點P作
,點P為直線AB下方拋物線上一動點,過點P作![]() 于D,連接AP.
于D,連接AP.
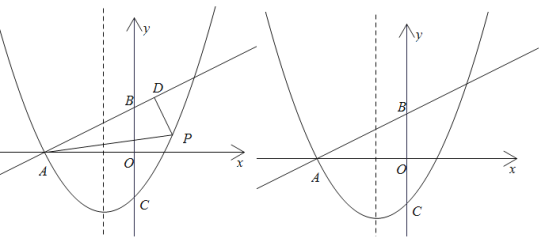
(1)求拋物線的解析式;
(2)若以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點P的坐標(biāo);
相似,求點P的坐標(biāo);
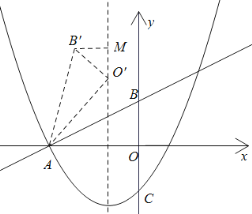
(3)將![]() 繞點A旋轉(zhuǎn),當(dāng)點O的對應(yīng)點
繞點A旋轉(zhuǎn),當(dāng)點O的對應(yīng)點![]() 落在拋物線的對稱軸上時,請直接寫出點B的對應(yīng)點
落在拋物線的對稱軸上時,請直接寫出點B的對應(yīng)點![]() 的坐標(biāo).
的坐標(biāo).
【答案】(1)![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時三角形相似;(3)點
時三角形相似;(3)點![]() 的坐標(biāo)為
的坐標(biāo)為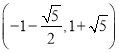 或
或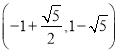 .
.
【解析】
(1)先求出A,B的坐標(biāo),然后根據(jù)拋物線![]() 經(jīng)過點A,C,解出a,c的值,即可求出拋物線解析式;
經(jīng)過點A,C,解出a,c的值,即可求出拋物線解析式;
(2)分①當(dāng)![]() 時和②當(dāng)
時和②當(dāng)![]() 時兩種情況討論即可;
時兩種情況討論即可;
(3)先將拋物線的解析式化為頂點式,得出拋物線的對稱軸為:x=-1,根據(jù)![]() ,得出AO=3,BO=
,得出AO=3,BO=![]() ,然后設(shè)O
,然后設(shè)O![]() (-1,m),解出m值,分①當(dāng)O
(-1,m),解出m值,分①當(dāng)O![]() (-1,
(-1,![]() )時和②當(dāng)O
)時和②當(dāng)O![]() (-1,-
(-1,-![]() )時兩種情況討論即可.
)時兩種情況討論即可.
(1)∵直線![]() 交
交![]() 軸于A,B,
軸于A,B,
![]() ,
,
∵拋物線![]() 經(jīng)過點A,C,
經(jīng)過點A,C,
∴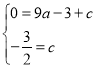 ,
,
解得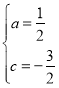 ,
,
∴拋物線解析式為![]() ;
;
(2)①當(dāng)![]() 時,點P為拋物線與x軸的交點,
時,點P為拋物線與x軸的交點,
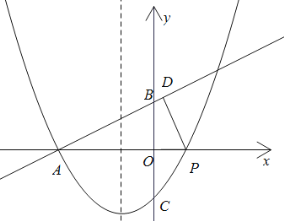
令![]() ,
,
解得![]() (舍去)
(舍去)
∴點P的坐標(biāo)為![]() ;
;
②當(dāng)![]() 時,
時,![]() ,
,
![]() ,
,
過點B作![]() ,且使得
,且使得![]() ,則P點必在直線AE與拋物線的交點上,
,則P點必在直線AE與拋物線的交點上,
做![]() 軸于點F,
軸于點F,
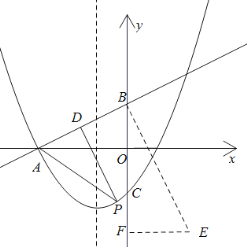
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
設(shè)直線AE的解析式為![]()
則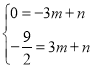 ,
,
解得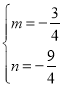 ,
,
∴直線AE的解析式為![]() ,
,
解方程組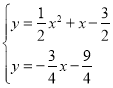
解得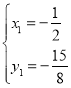 ,
,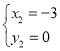 ,
,
∴點P的坐標(biāo)為![]() ,
,
∴當(dāng)![]() 或(1,0)時三角形相似;
或(1,0)時三角形相似;
(3)由題拋物線的解析式為![]() ,
,
∴拋物線的對稱軸為:x=-1,
∵![]() ,
,
∴AO=3,BO=![]() ,
,
∴設(shè)O![]() (-1,m),
(-1,m),
則有AO![]() =
=![]() =AO=3,
=AO=3,
解得:m=![]() 或m=
或m=![]() ,
,
①當(dāng)O![]() (-1,
(-1,![]() )時,
)時,
設(shè)AO![]() 的解析式為:y=ax+b,
的解析式為:y=ax+b,
將A(-3,0),O![]() (-1,
(-1,![]() )代入得
)代入得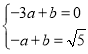 ,
,
解得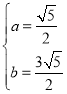 ,
,
∴AO![]() 的解析式為:y=
的解析式為:y=![]() x+
x+![]() ,
,
∵B![]() O
O![]() ⊥AO
⊥AO![]() ,
,
∴可設(shè)B![]() O
O![]() 的解析式為:y=
的解析式為:y=![]() x+b1,
x+b1,
將O![]() (-1,
(-1,![]() )代入得
)代入得![]() =
=![]() ×(-1)+b1,
×(-1)+b1,
解得b1=![]() ,
,
∴B![]() O
O![]() 的解析式為:y=
的解析式為:y=![]() x+
x+![]() ,
,
設(shè)B![]() 的坐標(biāo)為(x,
的坐標(biāo)為(x,![]() x+
x+![]() ),
),
則B![]() O
O![]() =
=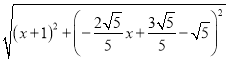 =BO=
=BO=![]() ,
,
解得x1=-1-![]() ,x2=-1-
,x2=-1-![]() (不符合此時的情況,舍去),
(不符合此時的情況,舍去),
將x1代入![]() x+
x+![]() =1+
=1+![]() ,
,
∴B![]() 的坐標(biāo)為(-1-
的坐標(biāo)為(-1-![]() ,1+
,1+![]() );
);
②當(dāng)O![]() (-1,-
(-1,-![]() )時,
)時,
同理可得B![]() 的坐標(biāo)為(-1+
的坐標(biāo)為(-1+![]() ,1-
,1-![]() );
);
綜上:點![]() 的坐標(biāo)為
的坐標(biāo)為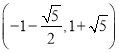 或
或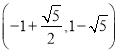 .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數(shù)學(xué) 來源: 題型:
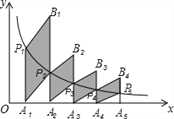
【題目】如圖,分別過反比例函數(shù)y=![]() 的圖象上的點P1(1,y1),P2(2,y2),…Pn(n,yn)…作x軸的垂線,垂足分別為A1,A2,…,An…,連接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2為一組鄰邊畫一個平行四邊形A1P1B1P2,以A 2P2,A2P3為一組鄰邊畫一個平行四邊形A2P2B2P3,點B2的縱坐標(biāo)是____.依此類推,則點Bn的縱坐標(biāo)是_______.(結(jié)果用含n代數(shù)式表示)
的圖象上的點P1(1,y1),P2(2,y2),…Pn(n,yn)…作x軸的垂線,垂足分別為A1,A2,…,An…,連接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2為一組鄰邊畫一個平行四邊形A1P1B1P2,以A 2P2,A2P3為一組鄰邊畫一個平行四邊形A2P2B2P3,點B2的縱坐標(biāo)是____.依此類推,則點Bn的縱坐標(biāo)是_______.(結(jié)果用含n代數(shù)式表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知![]() 是銳角三角形
是銳角三角形![]() .
.

(1)請在圖1中用無刻度的直尺和圓規(guī)作圖;作直線![]() ,使
,使![]() 上的各點到
上的各點到![]() 、
、![]() 兩點的距離相等;設(shè)直線
兩點的距離相等;設(shè)直線![]() 與
與![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() ,作一個圓,使得圓心
,作一個圓,使得圓心![]() 在線段
在線段![]() 上,且與邊
上,且與邊![]() 、
、![]() 相切;(不寫作法,保留作圖痕跡)
相切;(不寫作法,保留作圖痕跡)
(2)在(1)的條件下,若![]() ,
,![]() ,則
,則![]() 的半徑為________.
的半徑為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
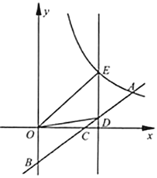
【題目】如圖,在平面直角坐標(biāo)系![]() 中,反比例函數(shù)
中,反比例函數(shù)![]() 的圖像經(jīng)過點
的圖像經(jīng)過點![]() ,點
,點![]() 在
在![]() 軸的負(fù)半軸上,
軸的負(fù)半軸上,![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
(1)![]() ________,點
________,點![]() 的坐標(biāo)為________;
的坐標(biāo)為________;
(2)若點![]() 為線段
為線段![]() 上的一個動點,過點
上的一個動點,過點![]() 作
作![]() 軸,交反比例函數(shù)圖像于點
軸,交反比例函數(shù)圖像于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
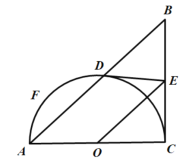
【題目】在![]() 中,
中,![]() ,以AC為直徑的半圓O交于點D,過點D作圓O的切線,交BC于點E,點F是半圓上異于點D的任一動點.
,以AC為直徑的半圓O交于點D,過點D作圓O的切線,交BC于點E,點F是半圓上異于點D的任一動點.
(1)求證:![]() ;
;
(2)填空:
①若![]() ,則四邊形
,則四邊形![]() 的面積為________;
的面積為________;
②當(dāng)![]() 的度數(shù)是_______時,以
的度數(shù)是_______時,以![]() 為頂點的四邊形為菱形.
為頂點的四邊形為菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩家商場平時以同樣價格出售相同的商品,新冠疫情期間,為了減少庫存,甲、乙兩家商場打折促銷,甲商場所有商品按9折出售,乙商場對一次購物中超過100元后的價格部分打8折.
⑴.以![]() (單位:元)表示商品原價,
(單位:元)表示商品原價,![]() (單位:元)表示實際購物金額,分別就兩家商場的讓利方式寫出
(單位:元)表示實際購物金額,分別就兩家商場的讓利方式寫出![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
⑵.新冠疫情期間如何選擇這兩家商場去購物更省錢?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
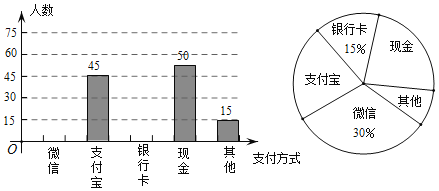
【題目】隨著科技的迅猛發(fā)展,人們?nèi)ド虉鲑徫锏闹Ц斗绞礁佣鄻印⒈憬荩承?shù)學(xué)興趣小組設(shè)計了一份“你最喜歡的支付方式”調(diào)查問卷(每人必選且只選一種),在某商場隨機(jī)調(diào)查了部分顧客,并將統(tǒng)計結(jié)果繪制成如下兩幅不完整的統(tǒng)計圖,請結(jié)合圖中所給的信息解答下列問題:
(1)這次活動共調(diào)查了 人,在扇形統(tǒng)計圖中,表示“現(xiàn)金”支付的扇形圓心角的度數(shù)為 ;
(2)將條形統(tǒng)計圖補(bǔ)充完整.觀察此圖,支付方式的“眾數(shù)”是 ;
(3)運(yùn)用這次的調(diào)查結(jié)果估計1000名顧客中用“支付寶”支付的有多少人?
(4)在一次購物中,嘉嘉和琪琪都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進(jìn)行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】火鍋是重慶的一張名片,深受廣大市民的喜愛.重慶某火鍋店采取堂食、外賣、店外擺攤(簡稱擺攤)三種方式經(jīng)營,6月份該火鍋店堂食、外賣、擺攤?cè)N方式的營業(yè)額之比為3:5:2.隨著促進(jìn)消費政策的出臺,該火鍋店老板預(yù)計7月份總營業(yè)額會增加,其中擺攤增加的營業(yè)額占總增加的營業(yè)額的![]() ,則擺攤的營業(yè)額將達(dá)到7月份總營業(yè)額的
,則擺攤的營業(yè)額將達(dá)到7月份總營業(yè)額的![]() ,為使堂食、外賣7月份的營業(yè)額之比為8:5,則7月份外賣還需增加的營業(yè)額與7月份總營業(yè)額之比是__________.
,為使堂食、外賣7月份的營業(yè)額之比為8:5,則7月份外賣還需增加的營業(yè)額與7月份總營業(yè)額之比是__________.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com