
【題目】如圖:點E、F為線段BD的兩個三等分點,四邊形AECF是菱形,且菱形AECF的周長為20,BD為24,則四邊形ABCD的面積為( )
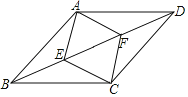
A.24B.36C.72D.144
【答案】C
【解析】
根據菱形的對角線互相垂直平分可得AC⊥BD,AO=OC,EO=OF,再求出BO=OD,證明四邊形ABCD是菱形,根據菱形的四條邊都相等求出邊長AE,根據菱形的對角線互相平分求出OE,然后利用勾股定理列式求出AO,再求出AC,最后根據四邊形的面積等于對角線乘積的一半列式計算即可得解.
解:如圖,連接AC交BD于點O,
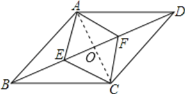
∵四邊形AECF是菱形,
∴AC⊥BD,AO=OC,EO=OF,
又∵點E、F為線段BD的兩個三等分點,
∴BE=FD,
∴BO=OD,
∵AO=OC,
∴四邊形ABCD為平行四邊形,
∵AC⊥BD,
∴四邊形ABCD為菱形;
∵四邊形AECF為菱形,且周長為20,
∴AE=5,
∵BD=24,點E、F為線段BD的兩個三等分點,
∴EF=8,OE=![]() EF=
EF=![]() ×8=4,
×8=4,
由勾股定理得,AO=![]() =
=![]() =3,
=3,
∴AC=2AO=2×3=6,
∴S四邊形ABCD=![]() BDAC=
BDAC=![]() ×24×6=72;
×24×6=72;
故選:C.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AC為直徑的⊙O交BC于點D,交AB于點E,過點D作DF⊥AB,垂足為F,連接DE.
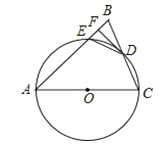
(1)求證:直線DF與⊙O相切;
(2)若AE=7,BC=6,求AC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2﹣2x+3與x軸交于A、B兩點,與y軸交于C點,M點在拋物線的對稱軸上,當點M到點B的距離與到點C的距離之和最小時,點M的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】爸爸想送小明一個書包和一輛自行車作為新年禮物,在甲、乙兩商場都發現同款的自行車單價相同,書包單價也相同,自行車和書包單價之和為452元,且自行車的單價比書包的單價4倍少8元.
(1)求自行車和書包單價各為多少元;
(2)新年來臨趕上商家促銷,乙商場所有商品打八五折(即8.5折)銷售,甲全場購物毎滿100元返購物券30元(即不足100元不返券,滿100元送30元購物券,滿200元送60元購物券),并可當場用于購物,購物券全場通用.但爸爸只帶了400元錢,如果他只在同一家商場購買看中的兩樣物品,在哪一家買更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
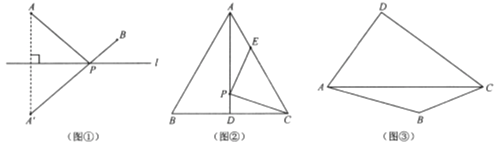
【題目】【新知理解】
如圖①,若點![]() 、
、![]() 在直線l同側,在直線l上找一點
在直線l同側,在直線l上找一點![]() ,使
,使![]() 的值最小.
的值最小.
作法:作點![]() 關于直線l的對稱點
關于直線l的對稱點![]() ,連接
,連接![]() 交直線l于點
交直線l于點![]() ,則點
,則點![]() 即為所求.
即為所求.
【解決問題】
如圖②,![]() 是邊長為6cm的等邊三角形
是邊長為6cm的等邊三角形![]() 的中線,點
的中線,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,則
上,則![]() 的最小值為 cm;
的最小值為 cm;
【拓展研究】
如圖③,在四邊形![]() 的對角線
的對角線![]() 上找一點
上找一點![]() ,使
,使![]() .(保留作圖痕跡,并對作圖方法進行說明)
.(保留作圖痕跡,并對作圖方法進行說明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“朗讀者”節目激發了同學們的讀書熱情,為了引導學生“多讀書,讀好書”,某校對八年級部分學生的課外閱讀量進行了隨機調查,整理調查結果發現,學生課外閱讀的本數最少的有5本,最多的有8本,并根據調查結果繪制了不完整的圖表:
本數(本) | 人數(人數) | 百分比 |
5 | a | 0.2 |
6 | 18 | 0.36 |
7 | 14 | b |
8 | 8 | 0.16 |
合計 | c | 1 |
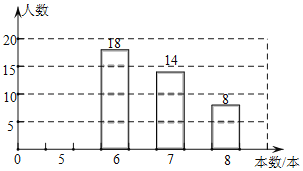
根據以上提供的信息,解答下列問題:
(1)a=_____,b=_____,c=______;
(2)補全上面的條形統計圖;
(3)若該校八年級共有1200名學生,請你分析該校八年級學生課外閱讀7本及以上的有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】情境![]() :小芳離開家去學校上學,走了一段路后,發現自己作業本忘家里了,于是返回家里找到作業本,然后又趕快去學校;
:小芳離開家去學校上學,走了一段路后,發現自己作業本忘家里了,于是返回家里找到作業本,然后又趕快去學校;
情境![]() :小明從家出發去圖書館還書,走了一段路程后,發現時間有點緊張,便以更快的速度前進.
:小明從家出發去圖書館還書,走了一段路程后,發現時間有點緊張,便以更快的速度前進.

(1)情境![]() 所對應的函數圖象分別是_______,_______(填寫序號);
所對應的函數圖象分別是_______,_______(填寫序號);
(2)請你為剩下的函數圖象寫出一個適合的情景.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答下列問題:
(1)閱讀理解:
如圖1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 邊上的中線
邊上的中線![]() 的取值范圍.
的取值范圍.
解決此問題可以用如下方法:延長![]() 到點
到點![]() 使
使![]() ,再連接
,再連接![]() (或將
(或將![]() 繞著
繞著![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三邊的關系即可判斷.中線
中,利用三角形三邊的關系即可判斷.中線![]() 的取值范圍是______.
的取值范圍是______.
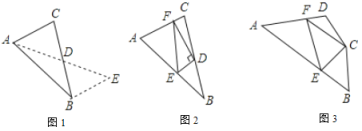
(2)問題解決:
如圖2,在![]() 中,
中,![]() 是
是![]() 邊上的中點,
邊上的中點,![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,求證:
,求證:![]() .
.
(3)問題拓展:
如圖3,在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 為頂點作一個
為頂點作一個![]() 角,角的兩邊分別交
角,角的兩邊分別交![]() ,
,![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() ,探索線段
,探索線段![]() ,
,![]() ,
,![]() 之間的數量關系,并加以證明.
之間的數量關系,并加以證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC,∠C=90°,AC=12,BC=6,一條線段PQ=AB,P、Q兩點分別在AC和過點A且垂直于AC的射線AX上運動,要使△ABC和△QPA全等,則AP= ______ .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com