
【題目】如圖直角坐標(biāo)系中,已知A(-8,0),B(0,6),點(diǎn)M在線段AB上.
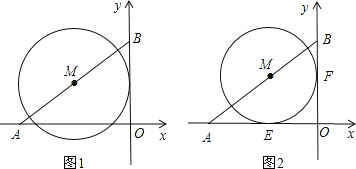
(1)如圖1,如果點(diǎn)M是線段AB的中點(diǎn),且⊙M的半徑為4,試判斷直線OB與⊙M的位置關(guān)系,并說明理由;
(2)如圖2,⊙M與x軸、y軸都相切,切點(diǎn)分別是點(diǎn)E、F,試求出點(diǎn)M的坐標(biāo).
【答案】(1)直線OB與⊙M相切.;(2)M的坐標(biāo)為(-![]() ,
,![]() ).
).
【解析】
試題(1)設(shè)線段OB的中點(diǎn)為D,證明MD=4,且MD⊥OB即可;
(2)先利用待定系數(shù)法求得直線AB的解析式:![]() ,根據(jù)切線的性質(zhì)得到點(diǎn)M到x軸、y軸的距離都相等,設(shè)M(a,-a)(-8<a<0).代入
,根據(jù)切線的性質(zhì)得到點(diǎn)M到x軸、y軸的距離都相等,設(shè)M(a,-a)(-8<a<0).代入![]() ,即可求得a的值,即得到M的坐標(biāo).
,即可求得a的值,即得到M的坐標(biāo).
試題解析:(1)直線OB與⊙M相切.
理由:
設(shè)線段OB的中點(diǎn)為D,連結(jié)MD.
因?yàn)辄c(diǎn)M是線段AB的中點(diǎn),所以MD∥AO,MD=4.
所以∠AOB=∠MDB=900,
所以MD⊥OB,點(diǎn)D在⊙M上.
又因?yàn)辄c(diǎn)D在直線OB上,
所以直線OB與⊙M相切.
(2)可求得過點(diǎn)A、B的一次函數(shù)關(guān)系式是![]() ,
,
因?yàn)?/span>⊙M與x軸、y軸都相切,
所以點(diǎn)M到x軸、y軸的距離都相等.
設(shè)M(a,-a) (-8<a<0) .
把x=a,y=-a代入![]() ,
,
得-a=![]() a+6,得a=-
a+6,得a=-![]() .
.
所以點(diǎn)M的坐標(biāo)為(-![]() ,
,![]() ).
).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)y=![]() 是反比例函數(shù).
是反比例函數(shù).
(1)求m的值;
(2)指出該函數(shù)圖象所在的象限,在每個象限內(nèi),y隨x的增大如何變化?
(3)判斷點(diǎn)(![]() ,2)是否在這個函數(shù)的圖象上.
,2)是否在這個函數(shù)的圖象上.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
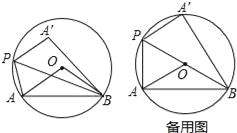
【題目】已知⊙O的半徑為2,∠AOB=120°.
(1)點(diǎn)O到弦AB的距離為 ;.
(2)若點(diǎn)P為優(yōu)弧AB上一動點(diǎn)(點(diǎn)P不與A、B重合),設(shè)∠ABP=α,將△ABP沿BP折疊,得到A點(diǎn)的對稱點(diǎn)為A′;
①若∠α=30°,試判斷點(diǎn)A′與⊙O的位置關(guān)系;
②若BA′與⊙O相切于B點(diǎn),求BP的長;
③若線段BA′與優(yōu)弧APB只有一個公共點(diǎn),直接寫出α的取值范圍.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=ax2﹣4ax+3a.
(Ⅰ)求該二次函數(shù)的對稱軸;
(Ⅱ)若該二次函數(shù)的圖象開口向下,當(dāng)1≤x≤4時,y的最大值是2,且當(dāng)1≤x≤4時,函數(shù)圖象的最高點(diǎn)為點(diǎn)P,最低點(diǎn)為點(diǎn)Q,求△OPQ的面積;
(Ⅲ)若對于該拋物線上的兩點(diǎn)P(x1,y1),Q(x2,y2),當(dāng)t≤x1≤t+1,x2≥5時,均滿足y1≥y2,請結(jié)合圖象,直接寫出t的最大值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線l1∥l2,⊙O與l1和l2分別相切于點(diǎn)A和點(diǎn)B.點(diǎn)M和點(diǎn)N分別是l1和l2上的動點(diǎn),MN沿l1和l2平移.⊙O的半徑為1,∠1=60°.有下列結(jié)論:①MN=![]() ;②若MN與⊙O相切,則AM=
;②若MN與⊙O相切,則AM=![]() ;③若∠MON=90°,則MN與⊙O相切;④l1和l2的距離為2,其中正確的有( )
;③若∠MON=90°,則MN與⊙O相切;④l1和l2的距離為2,其中正確的有( )
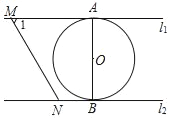
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)y=x2-2x-3的圖象與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,連接BC,點(diǎn)D為拋物線的頂點(diǎn),點(diǎn)P是第四象限的拋物線上的一個動點(diǎn)(不與點(diǎn)D重合).
(1)求∠OBC的度數(shù);
(2)連接CD,BD,DP,延長DP交x軸正半軸于點(diǎn)E,且S△OCE=S四邊形OCDB,求此時P點(diǎn)的坐標(biāo);
(3)過點(diǎn)P作PF⊥x軸交BC于點(diǎn)F,求線段PF長度的最大值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,Rt△ABC的直角邊BC在x軸正半軸上,斜邊AC邊上的中線BD反向延長線交y軸負(fù)半軸于E,雙曲線y=![]() (x>0)的圖象經(jīng)過點(diǎn)A,若△BEC的面積為6,則k等于( )
(x>0)的圖象經(jīng)過點(diǎn)A,若△BEC的面積為6,則k等于( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,將邊長為2cm的正方形ABCD沿其對角線AC剪開,再把△ABC沿著AD方向平移,得到△A′B′C′,若兩個三角形重疊部分的面積為1cm2,則它移動的距離AA′等于( )

A. 0.5cm B. 1cm C. 1.5cm D. 2cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長為1的正方形網(wǎng)格中,△ABC的頂點(diǎn)均在格點(diǎn)上,點(diǎn)A、B的坐標(biāo)分別是A(4,3)、B(4,1),把△ABC繞點(diǎn)C逆時針旋轉(zhuǎn)90°后得到△A1B1C.

(1)畫出△A1B1C,直接寫出點(diǎn)A1、B1的坐標(biāo);
(2)求在旋轉(zhuǎn)過程中,△ABC所掃過的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com