
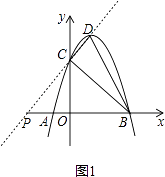
【題目】如圖,拋物線y=﹣x2+2x+3與x軸交于A,B兩點(diǎn),與y軸交于點(diǎn)C,點(diǎn)D為拋物線的頂點(diǎn),請(qǐng)解決下列問(wèn)題.
(1)填空:點(diǎn)C的坐標(biāo)為( , ),點(diǎn)D的坐標(biāo)為( , );
(2)設(shè)點(diǎn)P的坐標(biāo)為(a,0),當(dāng)|PD﹣PC|最大時(shí),求α的值并在圖中標(biāo)出點(diǎn)P的位置;
(3)在(2)的條件下,將△BCP沿x軸的正方向平移得到△B′C′P′,設(shè)點(diǎn)C對(duì)應(yīng)點(diǎn)C′的橫坐標(biāo)為t(其中0<t<6),在運(yùn)動(dòng)過(guò)程中△B′C′P′與△BCD重疊部分的面積為S,求S與t之間的關(guān)系式,并直接寫(xiě)出當(dāng)t為何值時(shí)S最大,最大值為多少?
【答案】
(1)0,3,1,4
(2)解:∵在三角形中兩邊之差小于第三邊,
∴延長(zhǎng)DC交x軸于點(diǎn)P,
設(shè)直線DC的解析式為y=kx+b,把D、C兩點(diǎn)坐標(biāo)代入可得 ![]() ,解得
,解得 ![]() ,
,
∴直線DC的解析式為y=x+3,
將點(diǎn)P的坐標(biāo)(a,0)代入得a+3=0,求得a=﹣3,
如圖1,點(diǎn)P(﹣3,0)即為所求;
(3)解:過(guò)點(diǎn)C作CE∥x,交直線BD于點(diǎn)E,如圖2,

由(2)得直線DC的解析式為y=x+3,
可求得直線BD的解析式為y=﹣2x+6,直線BC的解析式為y=﹣x+3,
在y=﹣2x+6中,當(dāng)y=3時(shí),x= ![]() ,
,
∴E點(diǎn)坐標(biāo)為( ![]() ,3),
,3),
設(shè)直線P′C′與直線BC交于點(diǎn)M,
∵P′C′∥DC,P′C′與y軸交于點(diǎn)(0,3﹣t),
∴直線P′C′的解析式為y=x+3﹣t,
聯(lián)立 ![]() ,解得
,解得 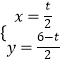 ,
,
∴點(diǎn)M坐標(biāo)為( ![]() ,
, ![]() ),
),
∵B′C′∥BC,B′坐標(biāo)為(3+t,0),
∴直線B′C′的解析式為y=﹣x+3+t,
分兩種情況討論:
①當(dāng)0<t< ![]() 時(shí),如圖2,B′C′與BD交于點(diǎn)N,
時(shí),如圖2,B′C′與BD交于點(diǎn)N,
聯(lián)立 ![]() ,解得
,解得 ![]() ,
,
∴N點(diǎn)坐標(biāo)為(3﹣t,2t),
S=S△B′C′P﹣S△BMP﹣S△BNB′= ![]() ×6×3﹣
×6×3﹣ ![]() (6﹣t)×
(6﹣t)× ![]() (6﹣t)﹣
(6﹣t)﹣ ![]() t×2t=﹣
t×2t=﹣ ![]() t2+3t,
t2+3t,
其對(duì)稱軸為t= ![]() ,可知當(dāng)0<t<
,可知當(dāng)0<t< ![]() 時(shí),S隨t的增大而增大,當(dāng)t=
時(shí),S隨t的增大而增大,當(dāng)t= ![]() 時(shí),有最大值
時(shí),有最大值 ![]() ;
;
②當(dāng) ![]() ≤t<6時(shí),如圖3,直線P′C′與DB交于點(diǎn)N,
≤t<6時(shí),如圖3,直線P′C′與DB交于點(diǎn)N,
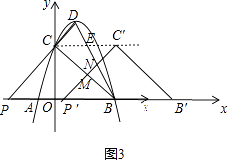
聯(lián)立 ![]() ,解得
,解得 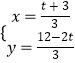 ,
,
∴N點(diǎn)坐標(biāo)為( ![]() ,
, ![]() ),
),
S=S△BNP′﹣S△BMP′= ![]() (6﹣t)×
(6﹣t)× ![]() ﹣
﹣ ![]() ×(6﹣t)×
×(6﹣t)× ![]() =
= ![]() (6﹣t)2=
(6﹣t)2= ![]() t2﹣t+3;
t2﹣t+3;
顯然當(dāng) ![]() <t<6時(shí),S隨t的增大而減小,當(dāng)t=
<t<6時(shí),S隨t的增大而減小,當(dāng)t= ![]() 時(shí),S=
時(shí),S= ![]()
綜上所述,S與t之間的關(guān)系式為S=  ,且當(dāng)t=
,且當(dāng)t= ![]() 時(shí),S有最大值,最大值為
時(shí),S有最大值,最大值為 ![]() .
.
【解析】解:(1)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴C(0,3),D(1,4),
所以答案是:0;3;1;4;



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】一個(gè)不透明的布袋里裝有16個(gè)只有顏色不同的球,其中紅球有x個(gè),白球有2x個(gè),其他均為黃球,現(xiàn)甲從布袋中隨機(jī)摸出一個(gè)球,若是紅球則甲同學(xué)勝,甲同學(xué)把摸出的球放回并攪勻,由乙同學(xué)隨機(jī)摸出一個(gè)球,若為黃球,則乙同學(xué)勝.
(1)當(dāng)x=3時(shí),誰(shuí)獲勝的可能性大?
(2)當(dāng)x為何值時(shí),游戲?qū)﹄p方是公平的?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,AB=2,AC=4,將△ABC繞點(diǎn)C按逆時(shí)針?lè)较蛐D(zhuǎn)得到△A′B′C,使CB′∥AB,分別延長(zhǎng)AB、CA′相交于點(diǎn)D,則線段BD的長(zhǎng)為 . 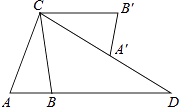
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】材料1:把一個(gè)多項(xiàng)式化成幾個(gè)整式的積的形式,這種變形叫做把這個(gè)多項(xiàng)式因式分解.例如:![]() ,
,![]() 都是因式分解.因式分解也可稱為分解因式.
都是因式分解.因式分解也可稱為分解因式.
材料2:只含有一個(gè)未知數(shù),且未知數(shù)的最高次數(shù)是![]() 的整式方程稱作一元二次方程.一元二次方程的般形式是:
的整式方程稱作一元二次方程.一元二次方程的般形式是:![]() (其中
(其中![]() ,
,![]() ,
,![]() 為常數(shù)且
為常數(shù)且![]() ).“轉(zhuǎn)化”是一種重要的數(shù)學(xué)思想方法,我們可以利用因式分解把部分一元二次方程轉(zhuǎn)化為一元一次方程求解.
).“轉(zhuǎn)化”是一種重要的數(shù)學(xué)思想方法,我們可以利用因式分解把部分一元二次方程轉(zhuǎn)化為一元一次方程求解.
例如解方程;![]()
![]()
![]()
![]() 或
或![]()
![]() 原方程的解是
原方程的解是![]() ,
,![]()
∴原方程的解是![]() ,
,![]()
又如解方程:![]()
![]()
![]()
![]()
![]() 原方程的解是
原方程的解是![]()
請(qǐng)閱讀以上材料回答以下問(wèn)題:
(1)若![]() ,則
,則![]() _______;
_______;![]() _______;
_______;
(2)請(qǐng)將下列多項(xiàng)式因式分解:
![]() _______,
_______,![]() ________;
________;
(3)在平面直角坐標(biāo)系中,已知點(diǎn)![]() ,
,![]() ,其中
,其中![]() 是一元二次方程
是一元二次方程![]() 的解,
的解,![]() 為任意實(shí)數(shù),求
為任意實(shí)數(shù),求![]() 長(zhǎng)度的最小值.
長(zhǎng)度的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在□ABCD的形外分別作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
連結(jié)AC、EF.在圖中找一個(gè)與△FAE全等的三角形,并加以證明.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,AB=6,AC=8,點(diǎn)D為邊BC的中點(diǎn),點(diǎn)M為邊AB上的一動(dòng)點(diǎn),點(diǎn)N為邊AC上的一動(dòng)點(diǎn),且∠MDN=90°,則cos∠DMN為( )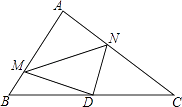
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)D在AC上,點(diǎn)F、G分別在AC、BC的延長(zhǎng)線上,CE平分∠ACB交BD于點(diǎn)O,且∠EOD+∠OBF=180°,∠F=∠G.則圖中與∠ECB相等的角有( )
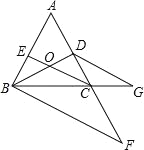
A. 6個(gè) B. 5個(gè) C. 4個(gè) D. 3個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四個(gè)結(jié)論①AH⊥EF,②∠ABF=∠EFB,③AC∥BE,④∠E=∠ABE.正確的是( )

A. ①②③④ B. ①② C. ①③④ D. ①②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】“校園安全”受到全社會(huì)的廣泛關(guān)注,某校政教處對(duì)部分學(xué)生及家長(zhǎng)就校園安全知識(shí)的了解程度,進(jìn)行了隨機(jī)抽樣調(diào)查,并繪制成如圖所示的兩幅統(tǒng)計(jì)圖,請(qǐng)根據(jù)統(tǒng)計(jì)圖中的信息,解答下列問(wèn)題:
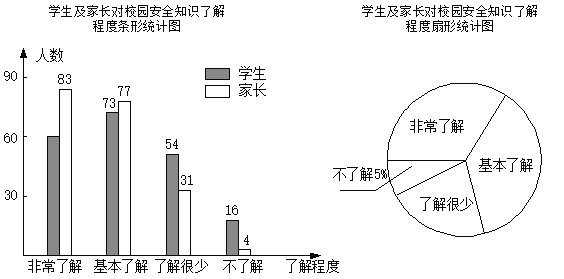
(1)參與調(diào)查的學(xué)生及家長(zhǎng)共有 人;
(2)在扇形統(tǒng)計(jì)圖中,“基本了解”所對(duì)應(yīng)的圓心角的度數(shù)是 ;
(3)在條形統(tǒng)計(jì)圖中,“非常了解”所對(duì)應(yīng)的學(xué)生人數(shù)是 ;
(4)若全校有1200名學(xué)生,請(qǐng)你估計(jì)對(duì)“校園安全”知識(shí)達(dá)到“非常了解”和“基本了解”的學(xué)生共有多少人.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com