
【題目】如圖,AB是⊙O的直徑,C是AB延長線上一點,CD與⊙O相切于點E,AD⊥CD于點D.
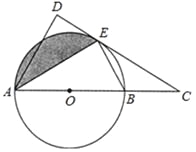
(1)求證:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的長;
②求出圖中陰影部分的面積.
科目:初中數學 來源: 題型:
【題目】有一個帶有進水管和出水管的容器,每分鐘進、出水量都是一定的,設從某一時刻開始的4分鐘內只進水,不出水,在隨后的8分鐘內既進水又出水,得到 時間x(分)與水量y(升)之間的關系圖.(如圖)
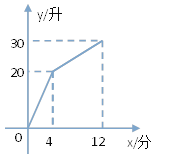
(1)每分鐘進水多少?
(2)0<x≤4時,y與x的函數關系式是什么?
(3)4<x≤12時,y與x的函數關系式是什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某縣盛產蘋果,春節期問,一外地經銷商安排![]() 輛汽年裝運
輛汽年裝運![]() 、
、![]() 、
、![]() 三種不同品質的蘋果
三種不同品質的蘋果![]() 噸到外地銷售,按計劃
噸到外地銷售,按計劃![]() 輛汽年都要裝滿且每輛汽車只能裝同一種品質的蘋果,每輛汽車的運載量及每噸蘋果的獲利如下表:
輛汽年都要裝滿且每輛汽車只能裝同一種品質的蘋果,每輛汽車的運載量及每噸蘋果的獲利如下表:
蘋果品種 |
|
|
|
每輛汽車運載數 |
|
|
|
每噸獲利(元) |
|
|
|
(1)設裝運![]() 種蘋果的車輛數為
種蘋果的車輛數為![]() 輛,裝運
輛,裝運![]() 種蘋果車輛數為
種蘋果車輛數為![]() 輛,據上表提供的信息,求出
輛,據上表提供的信息,求出![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)為了減少蘋果的積壓,縣林業局制定出臺了促進銷售的優惠政策,在外地經銷商原有獲利不變情況下,政府對外地經銷商按每噸![]() 元的標準實行運費補貼若
元的標準實行運費補貼若![]() 種蘋果的車輛數
種蘋果的車輛數![]() 滿足
滿足![]() .若要使該外地經銷商所獲利
.若要使該外地經銷商所獲利![]() (元)最大,應采用哪種車輛安排方案?并求出最大利潤
(元)最大,應采用哪種車輛安排方案?并求出最大利潤![]() (元)的最大值.
(元)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
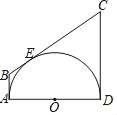
【題目】如圖,AB、CD分別與半圓OO切于點A,D,BC切⊙O于點E.若AB=4,CD=9,則⊙O的半徑為( )
A. 12 B. ![]()
![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,AC是⊙O的直徑,OB是⊙O的半徑,PA切⊙O于點A,PB與AC的延長線交于點M,∠COB=∠APB.
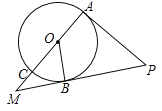
(1)求證:PB是⊙O的切線;
(2)當OB=3,PA=6時,求MB,MC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若關于x的一元二次方程x2+2x﹣m2﹣m=0(m>0),當m=1、2、3、…、2018時,相應的一元二次方程的兩個根分別記為α1、β1,α2、β2,…,α2018、β2018,則:![]() 的值為_____.
的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
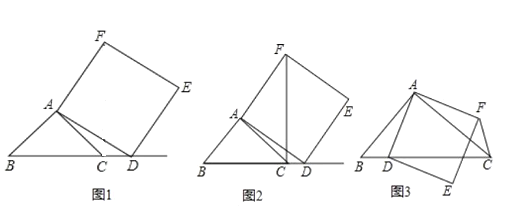
【題目】如圖①,在△ABC中,![]() 為銳角,點D為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF.
為銳角,點D為射線BC上一動點,連接AD,以AD為一邊且在AD的右側作正方形ADEF.
(1)如圖②,如果AB=AC,![]() ,當點D在線段BC的延長線上時,猜想線段CF、BD的關系,并說明理由.
,當點D在線段BC的延長線上時,猜想線段CF、BD的關系,并說明理由.
(2)如圖③,如果AB![]() AC,
AC,![]() 是銳角,點D在線段BC上,當
是銳角,點D在線段BC上,當![]() 時,必有CF
時,必有CF![]() BC(點C,F不重合),請先在橫線上添加條件,再作證明.
BC(點C,F不重合),請先在橫線上添加條件,再作證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近幾年石家莊霧霾天氣嚴重,給人們的生活帶來很大影響.某學校計劃在室內安裝空氣凈化裝置,需購進![]() ,
,![]() 兩種設備.每臺
兩種設備.每臺![]() 種設備價格比每臺
種設備價格比每臺![]() 種設備價格多1萬元,花50萬元購買的
種設備價格多1萬元,花50萬元購買的![]() 種設備和花70萬元購買
種設備和花70萬元購買![]() 種設備的數量相同.
種設備的數量相同.
(1)求![]() 種、
種、![]() 種設備每臺各多少萬元?
種設備每臺各多少萬元?
(2)根據單位實際情況,需購進![]() 、
、![]() 兩種設備共10臺,總費用不高于30萬元,求
兩種設備共10臺,總費用不高于30萬元,求![]() 種設備至少要購買多少臺?
種設備至少要購買多少臺?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com