
【題目】已知,如圖,在平面直角坐標系中,![]() 的斜邊BC在x軸上,直角頂點A在y軸的正半軸上,
的斜邊BC在x軸上,直角頂點A在y軸的正半軸上,![]() ,
,![]() .
.
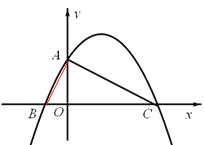
(1)求過A、B、C三點的拋物線的解析式和對稱軸;
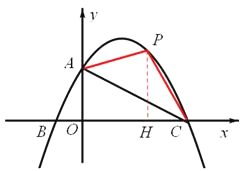
(2)設點![]() 是拋物線在第一象限部分上的點,
是拋物線在第一象限部分上的點,![]() 的面積為S,求S關于m的函數關系式,并求使S最大時點P的坐標;
的面積為S,求S關于m的函數關系式,并求使S最大時點P的坐標;
(3)在拋物線對稱軸上,是否存在這樣的點M,使得![]() 為等腰三角形(P為上述(2)問中使S最大時的點)?若存在,請直接寫出點M的坐標;若不存在,請說明理由;
為等腰三角形(P為上述(2)問中使S最大時的點)?若存在,請直接寫出點M的坐標;若不存在,請說明理由;
(4)設點M是直線AC上的動點,試問:在平面直角坐標系中,是否存在位于直線AC下方的點N,使得以點O、A、M、N為頂點的四邊形是菱形?若存在,求出點N的坐標;若不存在,說明理由.
【答案】(1)y=![]() ;對稱軸為x=
;對稱軸為x=![]() ;(2)S=-(m-2)2+4,點P的坐標為(2,3);(3)點M的坐標為(
;(2)S=-(m-2)2+4,點P的坐標為(2,3);(3)點M的坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )時,△MPC為等腰三角形;(4)點N的坐標為(
)時,△MPC為等腰三角形;(4)點N的坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(-2,1).
)或(-2,1).
【解析】
(1)由同角的余角相等得到一對角相等,再由一對直角相等,得到三角形AOB與三角形AOC相似,由相似得比例,求出OC的長,確定出C坐標,由B與C坐標設出拋物線的交點式解析式,將A坐標代入求出a的值,確定出拋物線解析式,求出對稱軸即可;
(2)連接AP,CP,過P作PQ垂直于x軸,將x=m代入拋物線解析式表示出P的縱坐標,即為PQ的長,三角形APC面積=梯形APQO面積+三角形PQC面積-三角形AOC面積,列出S關于m的二次函數解析式,利用二次函數的性質求出S最大時m的值,即可確定出此時P的坐標;
(3)分點M是頂點、點C是頂點、點P是頂點三種情況分別討論即可;
(4)分![]() 為邊、
為邊、![]() 為對角線分別進行討論即可.
為對角線分別進行討論即可.
(1)∵A(0,2),B(-1,0),
∴OA=2,OB=1,
∵∠AOB=∠AOC=∠BAC=90°,
∴∠ABO+∠BAO=90°,∠BAO+∠OAC=90°,
∴∠ABO=∠CAO,
∴△AOB∽△COA,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
設過![]() 、
、![]() 、
、![]() 三點的拋物線的解析式為
三點的拋物線的解析式為![]() ,
,
將![]() 代入,得
代入,得![]() ,解得
,解得![]() ,
,
∴過![]() 、
、![]() 、
、![]() 三點的拋物線的解析式為
三點的拋物線的解析式為![]() ,即
,即![]() ,
,
∵![]() ,
,
∴拋物線的對稱軸為![]() ;
;
(2)過點![]() 作
作![]() 軸的垂線,垂足為點
軸的垂線,垂足為點![]() ,
,
∵點![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
,
∴當![]() 時,
時,![]() 最大,
最大,
當![]() 時,
時,![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ;
;
(3)存在.
設點![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.
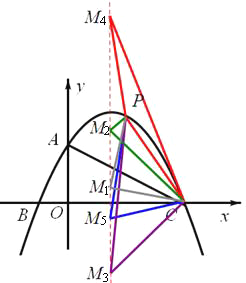
分三種情況討論:
①當點![]() 是頂點時,
是頂點時,![]() ,即
,即![]() ,解得,
,解得,![]() .
.
∴![]() ,
,
②當點![]() 是頂點時,
是頂點時,![]() ,即
,即![]() ,解得,
,解得,![]() .
.
∴![]() ,
,![]() ,
,
③當點![]() 是頂點時,
是頂點時,![]() ,即
,即![]() ,解得,
,解得,![]() .
.
∴![]() ,
,![]() ,
,
綜上所述,當點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]() 時,
時,![]() 為等腰三角形.
為等腰三角形.
(4)當![]() 為邊時,
為邊時,![]() ,
,![]() ,
,
若![]() 在
在![]() 右側時,則點
右側時,則點![]() 的坐標為
的坐標為![]() ;
;
若![]() 在
在![]() 左側時,則點
左側時,則點![]() 的坐標為
的坐標為![]() ,
,
當![]() 為對角線時,
為對角線時,![]() 垂直平分
垂直平分![]() ,則點
,則點![]() 的縱坐標為1,
的縱坐標為1,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
∴![]() ,
,
綜上所述,當點N的坐標為(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(-2,1).
)或(-2,1).


科目:初中數學 來源: 題型:
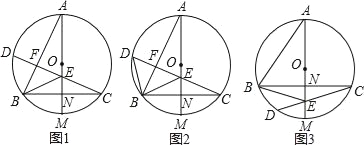
【題目】已知AM是⊙O直徑,弦BC⊥AM,垂足為點N,弦CD交AM于點E,連按AB和BE.
(1)如圖1,若CD⊥AB,垂足為點F,求證:∠BED=2∠BAM;
(2)如圖2,在(1)的條件下,連接BD,若∠ABE=∠BDC,求證:AE=2CN;
(3)如圖3,AB=CD,BE:CD=4:7,AE=11,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
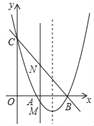
【題目】如圖,拋物線y=x2+bx+c與x軸交于點A和B(3,0),與y軸交于點C(0,3).
(1)求拋物線的解析式;
(2)若點M是拋物線上在x軸下方的動點,過M作MN∥y軸交直線BC于點N,求線段MN的最大值;
(3)E是拋物線對稱軸上一點,F是拋物線上一點,是否存在以A,B,E,F為頂點的四邊形是平行四邊形?若存在,請直接寫出點F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
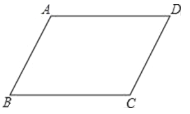
【題目】在一次數學活動中,黑板上畫著如圖所示的圖形,活動前老師在準備的四張卡片(大小、顏色、形狀相同)的正面上分別寫有如下四個等式中的一個等式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;小英同學閉上眼睛從四張卡片中隨機抽出一張,再從剩下的卡片中隨機抽出另一張,請結合圖形回答下列問題:
;小英同學閉上眼睛從四張卡片中隨機抽出一張,再從剩下的卡片中隨機抽出另一張,請結合圖形回答下列問題:
(1)當抽得②和④時,用②和④作條件能否判定四邊形是平行四邊形,請說明理由;
(2)請你用樹狀圖或表格表示抽取兩張卡片上的條件的所有可能出現的結果(用序號表示)并求以已經抽取的兩張卡片上的條件為已知,使四邊形不能構成平行四邊形的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著社會經濟的發展,汽車逐漸走入平常百姓家.某數學興趣小組隨機抽取了我市某單位部分職工進行調查,對職工購車情況分4類(A:車價40萬元以上;B:車價在20﹣40萬元;C:車價在20萬元以下;D:暫時未購車)進行了統計,并將統計結果繪制成以下條形統計圖和扇形統計圖.請結合圖中信息解答下列問題:

(1)調查樣本人數為 ,樣本中B類人數百分比是 ,其所在扇形統計圖中的圓心角度數是 ;
(2)把條形統計圖補充完整;
(3)該單位甲、乙兩個科室中未購車人數分別為2人和3人,現從這5個人中選2人去參觀車展,用列表或畫樹狀圖的方法,求選出的2人來自不同科室的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】寫字是學生的一項基本功,為了了解某校學生的書寫情況,隨機對該校部分學生進行測試,測試結果分為A,B,C,D四個等級.根據調查結果繪制了下列兩幅不完整的統計圖,請你根據統計圖提供的信息,回答以下問題:
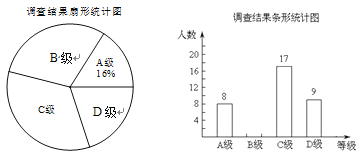
(1)把條形統計圖補充完整;
(2)若該校共有2000名學生,估計該校書寫等級為“D級”的學生約有 人;
(3)隨機抽取了4名等級為“A級”的學生,其中有3名女生,1名男生,現從這4名學生中任意抽取2名,用列表或畫樹狀圖的方法,求抽到的兩名學生都是女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖形的操作過程(本題中四個矩形的水平方向的邊長均為a,豎直方向的邊長均b):
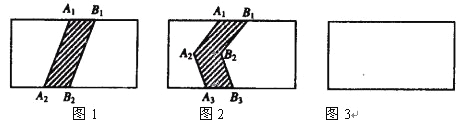
●在圖1中,將線段A1A2向右平移1個單位到B1B2,得到封閉圖形A1A2B2B1(即陰影部分);
●在圖2中,將折線A1A2A3向右平移1個單位到B1B2B3,得到封閉圖形A1A2A3B3B2B1(即陰影部分).
(1)在圖3中,請你類似地畫一條有兩個折點的線,同樣向右平移1個單位,從而得到一個封閉圖形,并用斜線畫出陰影;
(2)請你分別寫出上述三個圖形中除去陰影部分后剩余部分的面積:
S1=__________,S2=__________,S3=__________.
(3)聯想與探索
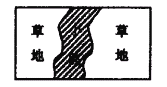
如上圖,在一塊矩形草地上,有一條彎曲的柏油小路(小路任何地方的水平寬度都是1個單位),請你猜想空白部分表示的草場地面積是多少?并說明你的猜想是正確的.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com