
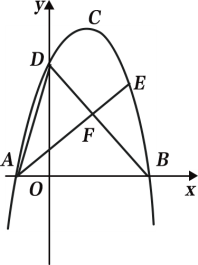
【題目】如圖1,拋物線![]() 的頂點為C(1,4),交x軸于A、B兩點,交y軸于點D,其中點B的坐標為(3,0).
的頂點為C(1,4),交x軸于A、B兩點,交y軸于點D,其中點B的坐標為(3,0).
(1)求拋物線的解析式;
(2)如圖2,點E是BD上方拋物線上的一點,連接AE交DB于點F,若AF=2EF,求出點E的坐標.
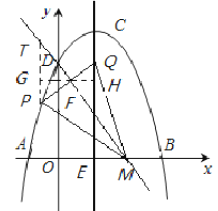
(3)如圖3,點M的坐標為(![]() ,0),點P是對稱軸左側拋物線上的一點,連接MP,將MP沿MD折疊,若點P恰好落在拋物線的對稱軸CE上,請求出點P的橫坐標.
,0),點P是對稱軸左側拋物線上的一點,連接MP,將MP沿MD折疊,若點P恰好落在拋物線的對稱軸CE上,請求出點P的橫坐標.


【答案】(1)![]() ;(2)E(2,3)或(1,4);(3)P點橫坐標為
;(2)E(2,3)或(1,4);(3)P點橫坐標為![]()
【解析】
(1) 拋物線![]() 的頂點為C(1,4),設拋物線的解析式為
的頂點為C(1,4),設拋物線的解析式為![]() ,由拋物線過點B,(3,0),即可求出a的值,即可求得解析式;
,由拋物線過點B,(3,0),即可求出a的值,即可求得解析式;
(2)過點E、F分別作x軸的垂線,交x軸于點M、N,設點E的坐標為![]() ,求出A、D點的坐標,得到OM=x,則AM=x+1,由AF=2EF得到
,求出A、D點的坐標,得到OM=x,則AM=x+1,由AF=2EF得到![]() ,從而推出點F的坐標
,從而推出點F的坐標![]() ,由
,由![]() ,列出關于x的方程求解即可;
,列出關于x的方程求解即可;
(3)先根據待定系數法求出直線DM的解析式為y=-2x+3,過點P作PT∥y軸交直線DM于點T,過點F作直線GH⊥y軸交PT于點G,交直線CE于點H.證明△FGP≌△FHQ,得到FG=FH,PT=![]() GH.設點P(m,-m+2m+3),則T(m,-2m+3),則PT=m-4m,GH=1-m,可得m-4m=
GH.設點P(m,-m+2m+3),則T(m,-2m+3),則PT=m-4m,GH=1-m,可得m-4m=![]() (1-m),解方程即可.
(1-m),解方程即可.
(1)∵拋物線的頂點為C(1,4),
∴設拋物線的解析式為![]() ,
,
∵拋物線過點B,(3,0),
∴![]() ,
,
解得a=-1,
∴設拋物線的解析式為![]() ,
,
即![]() ;
;
(2)如圖,過點E、F分別作x軸的垂線,交x軸于點M、N,設點E的坐標為![]() ,
,

∵拋物線的解析式為![]() ,
,
當y=0時, 解得x=-1或x=3, ∴A(-1.0), ∴點D(0,3), ∴過點BD的直線解析式為 則OM=x,AM=x+1, ∴ ∴ ∴ ∴ 解得x=1或x=2, ∴點E的坐標為(2,3)或(1,4); (3)設直線DM的解析式為y=kx+b,過點D(0,3),M( 可得, 解得k=-2,b=3, ∴直線DM的解析式為y=-2x+3, ∴ ∴tan∠DMO=2, 如圖,過點P作PT∥y軸交直線DM于點T,過點F作直線GH⊥y軸交PT于點G,交直線CE于點H. ∵PQ⊥MT, ∴∠TFG=∠TPF, ∴TG=2GF,GF=2PG, ∴PT= ∵PF=QF, ∴△FGP≌△FHQ, ∴FG=FH, ∴PT= 設點P(m,-m+2m+3),則T(m,-2m+3), ∴PT=m-4m,GH=1-m, ∴m-4m= 解得: ∴點P的橫坐標為![]() ,
,![]() ,點F在直線BD上,
,點F在直線BD上,![]() ,
,![]() ,
,![]() ,
,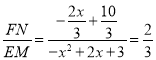 ,
,![]() ,0),
,0),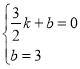 ,
,![]() ,
,![]() ,
,
![]() GF,
GF,![]() GH.
GH.![]() (1-m),
(1-m),![]() ,或
,或![]() (不合題意,舍去),
(不合題意,舍去),![]() .
.


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:
【題目】甲、乙兩校分別有一男一女共4名教師報名到農村中學支教.
(1)若從甲、乙兩校報名的教師中分別隨機選1名,則所選的2名教師性別相同的概率是 .
(2)若從報名的4名教師中隨機選2名,用列表或畫樹狀圖的方法求出這2名教師來自同一所學校的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是邊長為
是邊長為![]() 的等邊三角形,邊
的等邊三角形,邊![]() 在射線
在射線![]() 上,且
上,且![]() ,點
,點![]() 從點
從點![]() 出發,沿OM的方向以1cm/s的速度運動,當D不與點A重合時,將
出發,沿OM的方向以1cm/s的速度運動,當D不與點A重合時,將![]() 繞點C逆時針方向旋轉60°得到
繞點C逆時針方向旋轉60°得到![]() ,連接DE.
,連接DE.
(1)如圖1,求證:![]() 是等邊三角形;
是等邊三角形;
(2)如圖2,當6<t<10時,DE是否存在最小值?若存在,求出DE的最小值;若不存在,請說明理由.
(3)當點D在射線OM上運動時,是否存在以D,E,B為頂點的三角形是直角三角形?若存在,求出此時t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知有理數-3,1.
(1)在下列數軸上,標出表示這兩個數的點,并分別用A,B表示;
(2)若|m|=2,在數軸上表示數m的點,介于點A,B之間,在A的右側且到點B距離為5的點表示為n.
①計算m+n-mn;
②解關于x的不等式mx+4<n,并把解集表示在下列數軸上.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】濟寧某校為了解九年級學生藝術測試情況.以九年極(1)班學生的藝術測試成績為樣本,按![]() 、
、![]() 、
、![]() 、
、![]() 四個等級進行統計,并將統計結果繪制成如下的統計圖,請你結合圖中所給信息解答下列問題:
四個等級進行統計,并將統計結果繪制成如下的統計圖,請你結合圖中所給信息解答下列問題:

(說明:![]() 級:90分~100分;
級:90分~100分;![]() 級:75分~89分;
級:75分~89分;![]() 級60分~74分;
級60分~74分;![]() 級:60分以下)
級:60分以下)
(1)此次抽樣共調查了多少名學生?
(2)請求出樣本中![]() 級的學生人數,井補全條形統計圖;
級的學生人數,井補全條形統計圖;
(3)若該校九年級有1000名學生,請你用此樣本估計藝術測試中分數不低于75分的學生人數,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,拋物線![]() 的頂點為點
的頂點為點![]() ,與
,與![]() 軸的負半軸交于點
軸的負半軸交于點![]() ,直線
,直線![]() 交拋物線W于另一點
交拋物線W于另一點![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
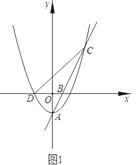
(1)求直線![]() 的解析式;
的解析式;
(2)過點![]() 作
作![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,若
,若![]() 平分
平分![]() ,求拋物線W的解析式;
,求拋物線W的解析式;
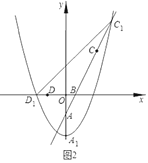
(3)若![]() ,將拋物線W向下平移
,將拋物線W向下平移![]() 個單位得到拋物線
個單位得到拋物線![]() ,如圖2,記拋物線
,如圖2,記拋物線![]() 的頂點為
的頂點為![]() ,與
,與![]() 軸負半軸的交點為
軸負半軸的交點為![]() ,與射線
,與射線![]() 的交點為
的交點為![]() .問:在平移的過程中,
.問:在平移的過程中,![]() 是否恒為定值?若是,請求出
是否恒為定值?若是,請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中(如圖),已知拋物線y=ax2+bx+c(a≠0)的圖象經過點B (4,0)、D (5,3),設它與x軸的另一個交點為A(點A在點B的左側),且△ABD的面積是3.
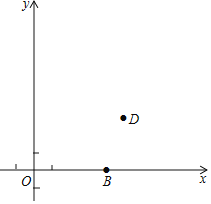
(1)求該拋物線的表達式;
(2)求∠ADB的正切值;
(3)若拋物線與y軸交于點C,直線CD交x軸于點E,點P在射線AD上,當△APE與△ABD相似時,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com