
【題目】如圖,AB為![]() 的直徑,AC,BC分別交
的直徑,AC,BC分別交![]() 于點E,D,
于點E,D,![]() ,
,![]() .現給出以下四個結論:①
.現給出以下四個結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確結論的序號是________.(填寫所有正確結論的序號)
.其中正確結論的序號是________.(填寫所有正確結論的序號)
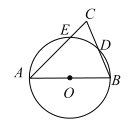
【答案】②④
【解析】
連結AD、BE,DE,如圖,根據圓周角定理得∠ADB=90°,則AD⊥BC,加上CD=BD,根據等腰三角形的判定即可得到AB=AC;再根據等腰三角形的性質和三角形內角和定理可計算出∠BAC=40°;由AB為直徑得到∠AEB=90°,則∠ABE=50°,根據圓周角定理可判斷![]() ;接著證明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等線段代換即可得到CECA=2BD2.
;接著證明△CED∽△CBA,利用相似比得到CECA=CDCB,然后利用等線段代換即可得到CECA=2BD2.
解:連結AD、BE,DE,如圖,
∵AB為直徑,
∴∠ADB=90°,
∴AD⊥BC,
而CD=BD,
∴AB=AC,所以②正確;
∵∠C=70°,
∴∠ABC=∠C=70°,
∴∠BAC=40°,所以①錯誤;
∵AB為直徑,
∴∠AEB=90°,
∴∠ABE=50°,
∴![]() ,所以③錯誤;
,所以③錯誤;
∵∠CED=∠CBA,
而∠C公共,
∴△CED∽△CBA,
∴![]() ,
,
∴CECA=CDCB,
∴CECA=BD2BD=2BD2,所以④正確.
故答案為②④.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
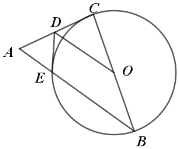
【題目】如圖,已知在![]() 中,
中,![]() ,以BC為直徑作
,以BC為直徑作![]() 交
交![]() 于點
于點![]() ,
,![]() 為AC邊的中點,連接
為AC邊的中點,連接![]() .
.
(1)求證:![]() 是
是![]() 的切線.
的切線.
(2)①若AC=3,AE=1,求![]() 的半徑;
的半徑;
②當![]() 時,四邊形
時,四邊形![]() 是正方形.
是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知正方形ABCD,E是線段BC上一點,N是線段BC延長線上一點,以AE為邊在直線BC的上方作正方形AEFG.
(1)連接GD,求證![]() ;
;
(2)連接FC,求![]() 的值;
的值;
(3)如圖2,將圖1中正方形ABCD改為矩形ABCD,![]() ,
,![]() ,E是線段BC上一動點(不含端點B,C),以AE為邊在直線BC的上方作矩形AEFG,使頂點G恰好落在射線CD上.當點E由B向C運動時,判斷
,E是線段BC上一動點(不含端點B,C),以AE為邊在直線BC的上方作矩形AEFG,使頂點G恰好落在射線CD上.當點E由B向C運動時,判斷![]() 的值是否為定值?若是,求出該定值;若不是,請說明理由.
的值是否為定值?若是,求出該定值;若不是,請說明理由.
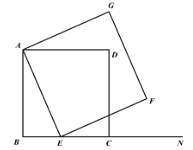
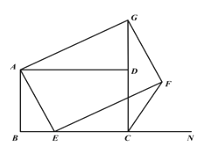
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,AB=26,以AB為直徑的⊙O交AC邊于點D,點E在BC上,連結BD,DE,∠CDE=∠ABD.
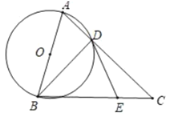
(1)證明:DE是⊙O的切線;
(2)若sin∠CDE=![]() ,求DC的長.
,求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 交
交![]() 軸于點
軸于點![]() 在
在![]() 軸正方向上取點
軸正方向上取點![]() ,使
,使![]() ;過點
;過點![]() 作
作![]() 軸,交
軸,交![]() 于點
于點![]() ,在
,在![]() 軸正方向上取點
軸正方向上取點![]() ,使
,使![]() ;過點
;過點![]() 作
作![]() 軸,交
軸,交![]() 于點
于點![]() ,在
,在![]() 軸正方向上取點
軸正方向上取點![]() ,使
,使![]() .記
.記![]() 面積為
面積為![]() ,
,![]() 面積為
面積為![]() 面積為
面積為![]() ,則
,則![]() 等于( )
等于( )
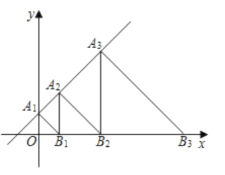
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】放風箏是大家喜愛的一種運動,星期天的上午小明在市政府廣場上放風箏.如圖,他在A處不小心讓風箏掛在了一棵樹梢上,風箏固定在了D處,此時風箏線AD與水平線的夾角為30°,為了便于觀察,小明迅速向前邊移動,收線到達了離A處10米的B處,此時風箏線BD與水平線的夾角為45°.已知點A,B,C在同一條水平直線上,請你求出小明此時所收回的風箏線的長度是多少米?(風箏線AD,BD均為線段,![]() ≈1.414,
≈1.414,![]() ≈1.732,最后結果精確到1米).
≈1.732,最后結果精確到1米).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com