
【題目】已知,平行四邊形![]() 中,連接
中,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() ,延長
,延長![]() 與
與![]() 相交于點
相交于點![]() .
.

(1)如圖1,若![]() ,
,![]() ,求線段
,求線段![]() 的長;
的長;
(2)如圖2,若![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() .求證:
.求證:![]() .
.
【答案】(1)AD=![]() ;(2)見解析
;(2)見解析
【解析】
(1)根據垂直的定義得到∠AEB=∠BEC=90°,根據勾股定理得到BE=![]() ,BC=
,BC=![]() ,根據平行四邊形的性質即可得到結果;
,根據平行四邊形的性質即可得到結果;
(2)推出△AEB是等腰直角三角形,得到∠ABE=45°,設∠CBE=x,根據等腰三角形的性質得到∠ABC=∠ACB=45°+x,求得∠EBC=22.5°,∠ACB=67.5°,推出A、B、C、F四點共圓,A、E、F、G四點共圓,得到∠CAF=∠CBE=22.5°,∠EGF=∠EAF=22.5°,求得∠AGE=67.5°,推出AE=GE,根據等腰直角三角形的性質即可得到結論.
(1)解:∵BE⊥AC,
∴∠AEB=∠BEC=90°,
∵AE=2,CE=1,
∴AC=AB=3,
∴BE=![]() =
=![]() ,
,
∴BC=![]() =
=![]() ,
,
∵四邊形ABCD是平行四邊形,
∴AD=BC=![]() ;
;
(2)證明:∵BE⊥AC,
∴∠AEB=∠BEC=90°,
∵∠BAC=45°,
∴△AEB是等腰直角三角形,
∴∠ABE=45°,AE=BE,
∵AB∥CD,
∴∠ACF=45°,∠ABC+∠DCB=180°,
設∠CBE=x,
∴∠ABC=45°+x,
∵AB=AC,
∴∠ABC=∠ACB=45°+x,
∵∠EBC+∠ECB=90°,
∴x+45°+x=90°,
∴x=22.5°,
∴∠EBC=22.5°,∠ACB=67.5°,
∵∠ABF=∠ACF=45°,
∴A、B、C、F四點共圓,
∴∠CAF=∠EBC=22.5°,
∵FG⊥AD,
∴∠AGF=∠AEF=90°,
∴A、E、F、G四點共圓,
∴∠EGF=∠EAF=22.5°,
∴∠AGE=67.5°,
∵∠CAD=∠ACB=67.5°,
∴∠EAG=∠AGE,
∴AE=GE,
∵AC=AB=![]() AE,
AE,
∴BE+EC=AE+EC=AC=![]() EG.
EG.


科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,O是坐標原點,矩形OACB的頂點A、B分別在![]() 軸和
軸和![]() 軸上,已知OA=5,OB=3,點D的坐標是(0,1),點P從點B出發以每秒1個單位的速度沿折線BCA的方向運動,當點P與點A重合時,運動停止,設運動的時間為
軸上,已知OA=5,OB=3,點D的坐標是(0,1),點P從點B出發以每秒1個單位的速度沿折線BCA的方向運動,當點P與點A重合時,運動停止,設運動的時間為![]() 秒.
秒.

(1)點P運動到與點C重合時,求直線DP的函數解析式;
(2)求△OPD的面積S關于![]() 的函數解析式,并寫出對應
的函數解析式,并寫出對應![]() 的取值范圍;
的取值范圍;
(3)點P在運動過程中,是否存在某些位置使△ADP是不以DP為底邊的等腰三角形,若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聯合國規定每年6月25日是“世界環境日”,某校編寫了關于環境保護的![]() 個問答題讓學生學習,為了解學生對
個問答題讓學生學習,為了解學生對![]() 個問答題的掌握情況,隨機抽查了部分學生進行答題測試,并根據測試結果得出下面兩個不完整的統計圖,請根據統計圖提供的信息,回答下列問題(其中
個問答題的掌握情況,隨機抽查了部分學生進行答題測試,并根據測試結果得出下面兩個不完整的統計圖,請根據統計圖提供的信息,回答下列問題(其中![]() 分別表示答對
分別表示答對![]() 個題,答對
個題,答對![]() 個題,答對
個題,答對![]() 個題,答對
個題,答對![]() 個題,答對
個題,答對![]() 個題的人數) :
個題的人數) :

(1)參加測試的學生有多少人?其中“答對個![]() 題”的有多少人數?
題”的有多少人數?
(2)把條形統計圖補充完整;
(3)若該校共有![]() 名學生,估計該校能“答對
名學生,估計該校能“答對![]() 個題”以上(含
個題”以上(含![]() 個題)的人數
個題)的人數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠BDC,∠2+∠3=180°.
(1) 請你判斷DA與CE的位置關系,并說明理由;
(2) 若DA平分∠BDC,CE⊥AE于點E,∠1=70°,試求∠FAB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】背景情境:
賽賽同學在學習《一元二次方程》中做過這樣一道題:
題目:已知實數![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
解:根據題意得
![]() 與
與![]() 為方程
為方程![]() 的兩根,
的兩根,
∴![]() ,
,![]()
∴![]()
請認真閱讀賽賽同學解題的方法,仔細思考.
解決問題:
(1)已知實數![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(2)設實數![]() 、
、![]() 分別滿足
分別滿足![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)已知關于![]() 的方程
的方程![]() 有兩個根
有兩個根![]() 、
、![]() 滿足
滿足![]() .當
.當![]() 的三邊
的三邊![]() 、
、![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,
,![]() (a≠b).求
(a≠b).求![]() 的值以及
的值以及![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A1,A2在射線OA上,B1在射線OB上,依次作A2B2∥A1B1 ,A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面積分別為1、9,則△A1007B1007A1008的面積是________.
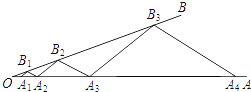
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在10×10的網格中,有一格點三角形ABC.(說明:頂點都在網格線交點處的三角形叫做格點三角形)

(1)將△ABC繞點C旋轉180°,得到△A′B′C,請直接畫出旋轉后的△A′B′C.(友情提醒:別忘了標上相應的字母!)
(2)在網格中以AB為一邊作格點△ABD(頂點在小正方形的頂點處的三角形稱為格點三角形),使它的面積是△ABC的2倍,則點D的個數有個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,E是BC邊的中點,連接DE并延長交AB的延長線于點F,則在題中條件下,下列結論不能成立的是( )
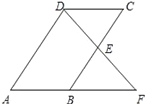
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com