
【題目】如圖1,直線![]() ,
,![]() 的平分線交
的平分線交![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)如圖2,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,探究
,探究![]() 與
與![]() 之間的數(shù)量關(guān)系,并證明你的猜想;
之間的數(shù)量關(guān)系,并證明你的猜想;
(3)如圖3,在(2)的條件下,![]() 的平分線交
的平分線交![]() 延長(zhǎng)線于點(diǎn)
延長(zhǎng)線于點(diǎn)![]() ,
,![]() 為
為![]() 延長(zhǎng)線上一點(diǎn),
延長(zhǎng)線上一點(diǎn),![]() ,將
,將![]() 延直線
延直線![]() 翻折,所得直線交
翻折,所得直線交![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的度數(shù).
的度數(shù).

【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據(jù)平行線的性質(zhì)定理得到內(nèi)錯(cuò)角相等,再根據(jù)角平分線的性質(zhì),即可得到等角.
(2)根據(jù)平行與垂直的性質(zhì),可得![]() ,而
,而![]() 為
為![]() 的外角,根據(jù)三角形的外角定理即可解答.
的外角,根據(jù)三角形的外角定理即可解答.
(3)根據(jù)題目中已給的數(shù)量關(guān)系, 求![]() 的度數(shù)可轉(zhuǎn)化為先求
的度數(shù)可轉(zhuǎn)化為先求![]() 的度數(shù),根據(jù)折疊的性質(zhì)和平行線的性質(zhì),可將多個(gè)角的復(fù)雜數(shù)量關(guān)系轉(zhuǎn)移到
的度數(shù),根據(jù)折疊的性質(zhì)和平行線的性質(zhì),可將多個(gè)角的復(fù)雜數(shù)量關(guān)系轉(zhuǎn)移到![]() 中,結(jié)果證明它是個(gè)等腰直角三角形,如此可解.
中,結(jié)果證明它是個(gè)等腰直角三角形,如此可解.
(1)證明: ![]()
![]() ,
,
![]()
![]() ,
,
又![]()
![]() 評(píng)分
評(píng)分![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
(2)![]()
![]() 為
為![]() 的外角,
的外角,
![]()
![]() ,
,
又![]()
![]()
![]()
![]() ,
,
即![]() .
.
(3)如圖,

根據(jù)折疊的性質(zhì), 
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 在
在![]() 中,
中, ![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 為等腰直角三角形,
為等腰直角三角形, ![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,將一副含30°和45°角的三角尺放置在直線![]() 上.
上.

(1)將圖1中的三角尺![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針方向旋轉(zhuǎn)至如圖2所示的位置,
順時(shí)針方向旋轉(zhuǎn)至如圖2所示的位置,![]() 在射線
在射線![]() 上,此時(shí)
上,此時(shí)![]() 旋轉(zhuǎn)的角度為度;
旋轉(zhuǎn)的角度為度;
(2)將圖2中的三角尺![]() 繞點(diǎn)
繞點(diǎn)![]() 順時(shí)針方向旋轉(zhuǎn)
順時(shí)針方向旋轉(zhuǎn)![]() (
(![]() ).
).
①如圖3,當(dāng)![]() 在
在![]() 的內(nèi)部時(shí),求
的內(nèi)部時(shí),求![]() 的值;
的值;
②若旋轉(zhuǎn)的速度為每秒15°,經(jīng)過![]() 秒,當(dāng)三角尺
秒,當(dāng)三角尺![]() 與三角尺
與三角尺![]() 的重疊部分以
的重疊部分以![]() 為頂點(diǎn)的角的度數(shù)為30°時(shí),求
為頂點(diǎn)的角的度數(shù)為30°時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校260名學(xué)生參加植樹活動(dòng),要求每人植4~7棵,活動(dòng)結(jié)束后隨機(jī)抽查了若干名學(xué)生每人的植樹量,并分為四種類型, A:4棵;B:5棵;C:6棵;D:7棵,將各類的人數(shù)繪制成扇形圖(如圖1)和條形圖(如圖2),請(qǐng)回答下列問題:
(1)在這次調(diào)查中D類型有多少名學(xué)生?
(2)寫出被調(diào)查學(xué)生每人植樹量的眾數(shù)、中位數(shù);
(3)求被調(diào)查學(xué)生每人植樹量的平均數(shù),并估計(jì)這260名學(xué)生共植樹多少棵?

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列說法:①垂直于同一直線的兩條直線互相平行;②兩個(gè)無理數(shù)的和是無理數(shù);③點(diǎn)![]() 一定不在第四象限;④平方根等于本身的數(shù)是
一定不在第四象限;④平方根等于本身的數(shù)是![]() 或
或![]() ;⑤若點(diǎn)
;⑤若點(diǎn)![]() 的坐標(biāo)滿足
的坐標(biāo)滿足![]() ,則點(diǎn)
,則點(diǎn)![]() 落在原點(diǎn)上;⑥如果兩個(gè)角的角平分線互為反向延長(zhǎng)線,則這兩個(gè)角為對(duì)頂角.正確個(gè)數(shù)是( )
落在原點(diǎn)上;⑥如果兩個(gè)角的角平分線互為反向延長(zhǎng)線,則這兩個(gè)角為對(duì)頂角.正確個(gè)數(shù)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下列信息材料
信息1:因?yàn)闊o理數(shù)是無限不循環(huán)小數(shù),因此無理數(shù)的小數(shù)部分我們不可能全部地寫出來,比如、![]() 、
、![]() 等,而常用的“……”或者“
等,而常用的“……”或者“![]() ”的表示方法都不夠百分百準(zhǔn)確;
”的表示方法都不夠百分百準(zhǔn)確;
信息2:![]() 的小數(shù)部分是
的小數(shù)部分是![]() ,可以看成
,可以看成![]() 得來的:
得來的:
信息3:任何一個(gè)無理數(shù),都可以夾在兩個(gè)相鄰的整數(shù)之間,如![]() ,是因?yàn)?/span>
,是因?yàn)?/span>![]() :
:
根據(jù)上述信息,回答下列問題:
(1)若![]() ,則
,則![]() 的小數(shù)部分可以表示為_______;
的小數(shù)部分可以表示為_______;
(2)![]() 也是夾在兩個(gè)整數(shù)之間的,可以表示為
也是夾在兩個(gè)整數(shù)之間的,可以表示為![]() 則
則![]() _______;
_______;
(3)若![]() ,其中
,其中![]() 是整數(shù),且
是整數(shù),且![]() ,請(qǐng)求
,請(qǐng)求![]() 的相反數(shù).
的相反數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,∠C>∠B,AE平分∠BAC,F(xiàn)為射線AE上一點(diǎn)(不與點(diǎn)E重合),且FD⊥BC于D;
(1)如果點(diǎn)F與點(diǎn)A重合,且∠C=50°,∠B=30°,如圖1,求∠EFD的度數(shù);
(2)如果點(diǎn)F在線段AE上(不與點(diǎn)A重合),如圖2,問∠EFD與∠C﹣∠B有怎樣的數(shù)量關(guān)系?并說明理由.
(3)如果點(diǎn)F在△ABC外部,如圖3,此時(shí)∠EFD與∠C﹣∠B的數(shù)量關(guān)系是否會(huì)發(fā)生變化?請(qǐng)說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】規(guī)定兩數(shù)a、b之間的一種運(yùn)算,記作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因?yàn)?/span>![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根據(jù)上述規(guī)定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究這種運(yùn)算時(shí)發(fā)現(xiàn)一個(gè)現(xiàn)象:![]() ,他給出了如下的證明:
,他給出了如下的證明:
設(shè)![]() ,則
,則![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
請(qǐng)你嘗試運(yùn)用上述這種方法說明下面這個(gè)等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 、
、![]() 、
、![]() 三點(diǎn)在同一條直線上,
三點(diǎn)在同一條直線上,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.
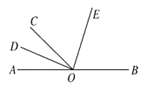
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,求
,求![]() ;
;
(3)![]() 是否隨
是否隨![]() 的度數(shù)的變化而變化?如果不變,度數(shù)是多少?請(qǐng)你說明理由,如果變化,請(qǐng)說明如何變化.
的度數(shù)的變化而變化?如果不變,度數(shù)是多少?請(qǐng)你說明理由,如果變化,請(qǐng)說明如何變化.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=8,AC=6.點(diǎn)D在邊AB上,AD=4.5.△ABC的角平分線AE交CD于點(diǎn)F.
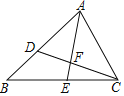
(1)求證:△ACD∽△ABC;
(2)求![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com