
【題目】如圖 (1),已知△ABC是等邊三角形,以BC為直徑的⊙O交AB、AC于D、E.求證:

(1)△DOE是等邊三角形.
(2)如圖(2),若∠A=60°,AB≠AC, 則(1)中結論是否成立?如果成立,請給出證明;如果不成立,請說明理由.
【答案】(1)證明見解析(2)當∠A=60°,AB≠AC時,(1)中的結論仍然成立
【解析】試題分析:(1)、根據等邊三角形的性質以及圓的半徑可以得出:△OBD和△OEC都為等邊三角形,結合∠BOD=∠EOC=60°得出∠DOE=60°,從而得出等邊三角形;(2)、連接CD,根據BC為直徑得出∠BDC=∠ADC=90°,根據∠A的度數得出∠ACD=30°,然后根據圓周角的性質可得:∠DOE=60°,結合OD=OE得出等邊三角形.
試題解析:(1)、證明:∵△ABC為等邊三角形, ∴∠B=∠C=60°,
∵OB=OC=OE=OD ,∴△OBD和△OEC都為等邊三角形,
∴∠BOD=∠EOC=60°, ∴∠DOE=60°, ∴△DOE為等邊三角形.
(2)、解:當∠A=60°,AB≠AC時,(1)中的結論仍然成立.
證明:連結CD,∵BC為⊙O的直徑, ∴∠BDC=90°, ∴∠ADC=90°, ∵∠A=60°,
∴∠ACD=30°, ∴∠DOE=2∠ACD=60°, ∵OD=OE ,∴△DOE為等邊三角形.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
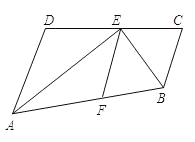
【題目】如圖,點E在線段CD上,EA、EB分別平分∠DAB和∠CBA,點F在線段AB上運動,AD=4cm,BC=3cm,且AD∥BC.
(1)你認為AE和BE有什么位置關系?并驗證你的結論;
(2)當點F運動到離點A多少厘米時,△ADE和△AFE全等?為什么?
(3)在(2)的情況下,此時BF=BC嗎?證明你的結論并求出AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,已知點C在線段AB上,且AC=6cm,BC=4cm,點M,N分別是AC,BC的中點,求線段MN的長度.
![]()
(2)在(1)中,如果AC=acm,BC=bcm,其它條件不變,你能猜出MN的長度嗎?請你用一句簡潔的話表述你發現的規律.
(3)對于(1)題,如果我們這樣敘述它:“已知線段AC=6cm,BC=4cm,點C在直線AB上,點M,N分別是AC,BC的中點,求MN的長度.”結果會有變化嗎?如果有,求出結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】Rt△ABC中,∠C=90°,點D,E分別是△ABC邊AC,BC上的點,點P是一動點.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若點P在線段AB上,如圖①所示,且∠α=50°,則∠1+∠2=________°;
(2)若點P在邊AB上運動,如圖②所示,則∠α,∠1,∠2之間的關系為:____________;

(3)若點P運動到邊AB的延長線上,如圖③所示,則∠α,∠1,∠2之間有何關系?猜想并說明理由;

(4)若點P運動到△ABC形外,如圖④所示,則∠α,∠1,∠2之間的關系為:____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年,我國海關總署嚴厲打擊“洋垃圾”違法行動,堅決把“洋垃圾”拒于國門之外.如圖,某天我國一艘海監船巡航到A港口正西方的B處時,發現在B的北偏東60°方向,相距150海里處的C點有一可疑船只正沿CA方向行駛,C點在A港口的北偏東30°方向上,海監船向A港口發出指令,執法船立即從A港口沿AC方向駛出,在D處成功攔截可疑船只,此時D點與B點的距離為75![]() 海里.
海里.
(1)求B點到直線CA的距離;
(2)執法船從A到D航行了多少海里?(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一塊長5米寬4米的地毯,為了美觀設計了兩橫、兩縱的配色條紋(圖中陰影部分),已知配色條紋的寬度相同,所占面積是整個地毯面積的![]() .
.
(1)求配色條紋的寬度;
(2)如果地毯配色條紋部分每平方米造價200元,其余部分每平方米造價100元,求地毯的總造價.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線l1∥l2,直線l3和直線l1,l2交于點C和D,直線l3上有一點P.
(1)如圖1,若P點在C,D之間運動時,問∠PAC,∠APB,∠PBD之間的關系是否發生變化,并說明理由;
(2)若點P在C,D兩點的外側運動時(P點與點C,D不重合,如圖2和3),試直接寫出∠PAC,∠APB,∠PBD之間的關系,不必寫理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有這樣一個問題:探究函數![]() 的圖象與性質.小美根據學習函數的經驗,對函數
的圖象與性質.小美根據學習函數的經驗,對函數![]() 的圖象與性質進行了探究.下面是小美的探究過程,請補充完整:
的圖象與性質進行了探究.下面是小美的探究過程,請補充完整:
(![]() )函數
)函數![]() 的自變量
的自變量![]() 的取值范圍是__________.
的取值范圍是__________.
(![]() )下表是
)下表是![]() 與
與![]() 的幾組對應值.
的幾組對應值.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
如圖,在平面直角坐標系![]() 中,描出以上表中各對對應值為坐標的點.
中,描出以上表中各對對應值為坐標的點.
根據描出的點,畫出該函數的圖象,標出函數的解析式.

(![]() )結合函數的圖象,寫出該函數的一條性質:__________.
)結合函數的圖象,寫出該函數的一條性質:__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車廠計劃一周生產自行車1400輛,平均每天生產200輛,但由于種種原因,實際每天生產量與計劃量相比有出入.下表是某周的生產情況(超產記為正、減產記為負):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減 | +5 | ﹣2 | ﹣4 | +12 | ﹣10 | +16 | ﹣9 |
(1)根據記錄的數據可知該廠星期六生產自行車______輛;
(2)根據記錄的數據可知該廠本周實際生產自行車_____輛;
(3)產量最多的一天比產量最少的一天多生產自行車_____輛;
(4)該廠實行每周計件工資制,每生產一輛車可得50元,若超額完成任務,則超過部分每輛另獎15元;少生產一輛扣20元,那么該廠工人這一周的工資總額是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com