
【題目】觀察下列等式:
3﹣![]() =3×
=3×![]() ;
;
(﹣![]() )﹣6=(﹣
)﹣6=(﹣![]() )×6;
)×6;
(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根據上面這些等式反映的規律,解答下列問題:
(1)上面等式反映的規律用文字語言可以描述如下:存在兩個有理數,使得這兩個有理數的差等于
.
(2)若滿足上述規律的兩個有理數中有一個數是![]() ,求另一個有理數;
,求另一個有理數;
(3)若這兩個有理數用字母a、b表示,則上面等式反映的規律用字母表示為 ;
(4)在(3)中的關系式中,字母a、b是否需要滿足一定的條件?若需要,直接寫出字母a、b應滿足的條件;若不需要,請說明理由.
【答案】(1)它們的積;(2)2或![]() ; (3)a-b=ab;(4)字母a,b應滿足的條件是倒數的差是1.
; (3)a-b=ab;(4)字母a,b應滿足的條件是倒數的差是1.
【解析】
(1)根據等式反映的規律用文字語言描述即可;
(2)根據規律求解即可;
(3)根據規律求解即可;
(4)根據等式的性質可得![]() =1,即字母a、b應滿足的條件是倒數的差是1,依此求解即可.
=1,即字母a、b應滿足的條件是倒數的差是1,依此求解即可.
(1)上面等式反映的規律用文字語言可描述為:存在兩個有理數,使得這兩個有理數的差等于它們的積,
故答案為:它們的積;
(2)∵2-![]() =2×
=2×![]() ,
,
∴另一個有理數為2;
(3)若這兩個有理數用字母a、b表示,則上面等式反映的規律用字母表示為a-b=ab;
(4)a-b=ab,
![]() ,
,
![]() =1,
=1,
故字母a、b應滿足的條件是倒數的差是1.


科目:初中數學 來源: 題型:
【題目】如圖,ABCD是矩形紙片,翻折∠B,∠D,使AD,BC邊與對角線AC重疊,且頂點B,D恰好落在同一點O上,折痕分別是CE,AF,則![]() 等于( )
等于( )

A. ![]() B. 2 C. 1.5 D.
B. 2 C. 1.5 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于A(﹣4,0),B(2,0),與y軸交于點C(0,2). 
(1)求拋物線的解析式;
(2)若點D為該拋物線上的一個動點,且在直線AC上方,當以A,C,D為頂點的三角形面積最大時,求點D的坐標及此時三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD是菱形,E是BD延長線上一點,F是DB延長線上一點,且DE=BF.請你以F為一個端點,和圖中已標明字母的某一點連成一條新的線段,猜想并證明它和圖中已有的某一條線段相等(只須證明一組線段相等即可).
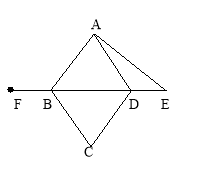
(1)連接 ;
(2)猜想: = ;
(3)證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,B是線段AD上一動點,沿A→D→A以 2 cm/s的速度往返運動1次,C是線段BD的中點,AD=10 cm,設點B的運動時間為t秒(0≤t≤10).
(1)當t=2時,
①AB=____cm;
②求線段CD的長度;
(2)用含t的代數式表示運動過程中AB的長;
(3)在運動過程中,若AB的中點為E,則EC的長是否變化?若不變,求出EC的長;若發生變化,請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點G,D,C在直線a上,點E,F,A,B在直線b上,若a∥b,Rt△GEF從如圖所示的位置出發,沿直線b向右勻速運動,直到EG與BC重合.運動過程中△GEF與矩形ABCD重合部分的面積(S)隨時間(t)變化的圖象大致是( )

A.  B.
B.  C.
C. 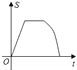 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
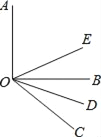
【題目】如圖所示,OE,OD分別平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度數;
(2)如果∠AOB=α,∠BOC=β(α、β均為銳角,α>β),其他條件不變,求∠DOE;
(3)從(1)、(2)的結果中,你發現了什么規律,請寫出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD∥BC,AF平分∠BAD交BC于點F,BE平分∠ABC交AD于點E.求證: 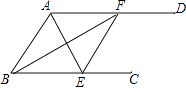
(1)△ABF是等腰三角形;
(2)四邊形ABFE是菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com