
【題目】已知關于x的一元二次方程x2﹣2(1﹣m)x+m2=0的兩實數根為x1 , x2 , 則y=x1+x2+2x1x2的最小值為 .
【答案】![]()
【解析】解:∵關于x的一元二次方程x2﹣2(1﹣m)x+m2=0有實數根,
∴△=[﹣2(1﹣m)]2﹣4m2=4﹣8m≥0,
∴m≤ ![]() .
.
∵關于x的一元二次方程x2﹣2(1﹣m)x+m2=0的兩實數根為x1,x2,
∴x1+x2=2(1﹣m),x1x2=m2,
∴y=x1+x2+2x1x2=2(1﹣m)+2m2=2m2﹣2m+2=2(m﹣ ![]() )2+
)2+ ![]() .
.
∵m≤ ![]() ,
,
∴當m= ![]() 時,y取最小值,最小值為
時,y取最小值,最小值為 ![]() .
.
所以答案是: ![]() .
.
【考點精析】認真審題,首先需要了解求根公式(根的判別式△=b2-4ac,這里可以分為3種情況:1、當△>0時,一元二次方程有2個不相等的實數根2、當△=0時,一元二次方程有2個相同的實數根3、當△<0時,一元二次方程沒有實數根),還要掌握根與系數的關系(一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A的坐標為![]() ,點B的坐標為
,點B的坐標為![]() ,點P在y軸上,當
,點P在y軸上,當![]() 的值最小時,P的坐標是
的值最小時,P的坐標是![]()
![]()
A. (0,1)B. (0,![]() )C. (0,0)D. (0,
)C. (0,0)D. (0,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市公交公司為應對春運期間的人流高峰,計劃購買A、B兩種型號的公交車共10輛,若購買A型公交車1輛,B型公交車2輛,共需400萬元;若購買A型公交車2輛,B型公交車3輛,共需650萬元,
(1)試問該公交公司計劃購買A型和B型公交車每輛各需多少萬元?
(2)若該公司預計在某條線路上A型和B型公交車每輛年均載客量分別為60萬人次和100萬人次.若該公司購買A型和B型公交車的總費用W不超過1200萬元,且確保這10輛公交車在某條線路的年均載客量總和不少于680萬人次,則該公司有哪幾種購車方案?哪種購車方案的總費用W最少?最少總費用是多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,BF平分∠ABC,交AD于點F,CE平分∠BCD,交AD于點E,AB=7,EF=3,則BC長為( )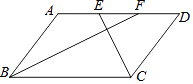
A.9
B.10
C.11
D.12
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com