
【題目】某學校為了慶祝校園藝術節,準備購買一批盆花布置校園.已知1盆A種花和2盆B種花一共需13元,2盆A種花和1盆B種花一共需11元.
(1)求1盆A種花和1盒B種花的售價各是多少元?
(2)學校準備購進這兩種盆花共100盆,并且A種盆花的數量不超過B種盆花數量的2倍,請求出A種盆花的數量最多是多少?
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,邊長為2的正方形ABCD在第一象限內,AB∥x軸,點A的坐標為(5,3),己知直線l:y= ![]() x﹣2
x﹣2
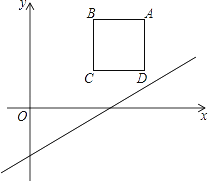
(1)將直線l向上平移m個單位,使平移后的直線恰好經過點A,求m的值
(2)在(1)的條件下,平移后的直線與正方形的邊長BC交于點E,求△ABE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,O為坐標原點.已知反比例函數y=![]() (k>0)的圖象經過點A(2,m),過點A作AB⊥x軸于點B,且△AOB的面積為
(k>0)的圖象經過點A(2,m),過點A作AB⊥x軸于點B,且△AOB的面積為![]() .
.
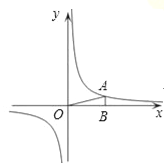
(1)求k和m的值;
(2)點C(x,y)在反比例函數y=![]() 的圖象上,求當1≤x≤3時函數值y的取值范圍;
的圖象上,求當1≤x≤3時函數值y的取值范圍;
(3)過原點O的直線l與反比例函數y=![]() 的圖象交于P、Q兩點,試根據圖象直接寫出線段PQ長度的最小值.
的圖象交于P、Q兩點,試根據圖象直接寫出線段PQ長度的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中是真命題的是( )
A. 兩條對角線相等的四邊形是矩形;
B. 有一條對角線平分一個內角的平行四邊形為菱形;
C. 對角線互相垂直且相等的四邊形是正方形;
D. 依次連結四邊形各邊的中點,所得四邊形是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是邊長為60cm的正方形硬紙片,剪掉陰影部分所示的四個全等的等腰直角三角形,再沿虛線折起,使A、B、C、D四個點重合于圖中的點P,正好形成一個底面是正方形的長方體包裝盒.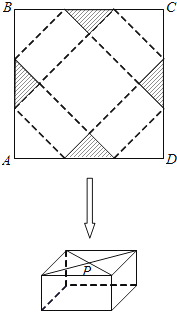
(1)若折疊后長方體底面正方形的面積為1250cm2 , 求長方體包裝盒的高;
(2)設剪掉的等腰直角三角形的直角邊長為x(cm),長方體的側面積為S(cm2),求S與x的函數關系式,并求x為何值時,S的值最大.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,在ABCD中,延長DA到點E,延長BC到點F,使得AE=CF,連接EF,分別交AB,CD于點M,N,連接DM,BN.
(1)求證:△AEM≌△CFN;
(2)求證:四邊形BMDN是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,對角線AC和BD相交于點O,如果AC=12、BD=10、AB=m,那么m的取值范圍是( )

A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD四條邊上的中點分別為E、F、G、H,順次連接EF、FG、GH、HE,得到四邊形EFGH(即四邊形ABCD的中點四邊形).
(1)四邊形EFGH的形狀是_____,證明你的結論;
(2)當四邊形ABCD的對角線滿足_____條件時,四邊形EFGH是矩形(不證明)
(3)你學過的哪種特殊四邊形的中點四邊形是矩形?_____(不證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了慶祝即將到來的“五四”青年節,某校舉行了書法比賽,賽后隨機抽查部分參賽同學的成績,并制作成圖表如下:
分數段 | 頻數 | 頻率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
請根據以上圖表提供的信息,解答下列問題:
(1)這次隨機抽查了 名學生;表中的數m= ,n= ;
(2)請在圖中補全頻數分布直方圖;
(3)若繪制扇形統計圖,分數段60≤x<70所對應扇形的圓心角的度數是 ;
(4)全校共有600名學生參加比賽,估計該校成績80≤x<100范圍內的學生有多少人?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com