
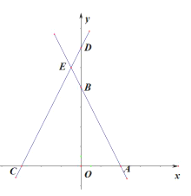
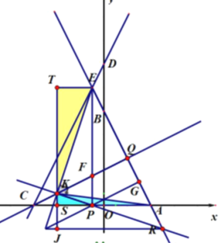
【題目】在平面直角坐標(biāo)系中,點(diǎn)O為坐標(biāo)原點(diǎn),直線![]() 與x,y軸分別交于點(diǎn)A,B兩點(diǎn),直線y=2x+3m與
與x,y軸分別交于點(diǎn)A,B兩點(diǎn),直線y=2x+3m與![]() 軸分別交于
軸分別交于![]() 兩點(diǎn),兩直線交于點(diǎn)E,點(diǎn)P在射線CA上,點(diǎn)Q在射線AE上,分別連接
兩點(diǎn),兩直線交于點(diǎn)E,點(diǎn)P在射線CA上,點(diǎn)Q在射線AE上,分別連接![]() 交于點(diǎn)F,且
交于點(diǎn)F,且![]() .
.
(1)若點(diǎn)E的橫坐標(biāo)為![]() ,求
,求![]() 的值
的值
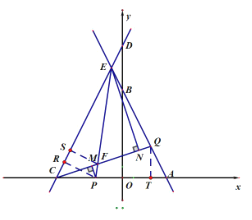
(2)當(dāng)![]() 時(shí),過(guò)點(diǎn)P作
時(shí),過(guò)點(diǎn)P作![]() 于點(diǎn)M,過(guò)點(diǎn)E作
于點(diǎn)M,過(guò)點(diǎn)E作![]() 于點(diǎn)N,求證:
于點(diǎn)N,求證:![]()
(3)在(1)的條件下,當(dāng)![]() 時(shí),過(guò)點(diǎn)P作
時(shí),過(guò)點(diǎn)P作![]() 交AB于點(diǎn)G,點(diǎn)K在射線CQ上,射線EK交直線
交AB于點(diǎn)G,點(diǎn)K在射線CQ上,射線EK交直線![]() 于點(diǎn)L,射線
于點(diǎn)L,射線![]() 交直線
交直線![]() 于點(diǎn)R,連接
于點(diǎn)R,連接![]() ,當(dāng)
,當(dāng)![]() 時(shí),求K點(diǎn)LR到的距離.
時(shí),求K點(diǎn)LR到的距離.
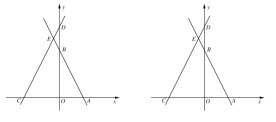
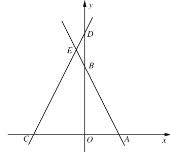
【答案】(1)m=4;(2)證明見(jiàn)解析;(3)![]() 或
或![]() .
.
【解析】
(1)根據(jù)![]() 點(diǎn)是兩直線的交點(diǎn),將
點(diǎn)是兩直線的交點(diǎn),將![]() 點(diǎn)的橫坐標(biāo)代入解析式建立等量關(guān)系即可求解;
點(diǎn)的橫坐標(biāo)代入解析式建立等量關(guān)系即可求解;
(2)分別作![]() ,根據(jù)函數(shù)解析式將
,根據(jù)函數(shù)解析式將![]() 點(diǎn)的坐標(biāo)表示出來(lái),再計(jì)算
點(diǎn)的坐標(biāo)表示出來(lái),再計(jì)算![]() 的正切值,從而得出
的正切值,從而得出![]() ,再根據(jù)函數(shù)解析式聯(lián)立解方程求表示出
,再根據(jù)函數(shù)解析式聯(lián)立解方程求表示出![]() 點(diǎn)坐標(biāo),表示出
點(diǎn)坐標(biāo),表示出![]() 的正弦值,設(shè)
的正弦值,設(shè)![]() ,表示出
,表示出![]() 、
、![]()
![]() ,以及
,以及![]() 的正切值,從而得出
的正切值,從而得出![]() ,可證
,可證![]() 設(shè)
設(shè)![]() 從而計(jì)算
從而計(jì)算![]() ,作
,作![]() 表示出
表示出![]() ,從而算出
,從而算出![]() ,
,![]() ,從而得證;
,從而得證;
(3)過(guò)![]() 作
作![]() 軸,過(guò)
軸,過(guò)![]() 作
作![]() ,由(1)得
,由(1)得![]() ,從而計(jì)算
,從而計(jì)算![]() 的函數(shù)解析式,得出
的函數(shù)解析式,得出![]() 的坐標(biāo),由(2)
的坐標(biāo),由(2)![]() ,得出
,得出![]() ,
,![]() ,
,![]() ,算出
,算出![]() 的函數(shù)解析式,再分類(lèi)討論:①設(shè)
的函數(shù)解析式,再分類(lèi)討論:①設(shè)![]()
![]() ,
,![]() 型可證
型可證![]() ,得出
,得出![]() ,從而計(jì)算
,從而計(jì)算![]() 的值和
的值和![]() 的坐標(biāo),所以
的坐標(biāo),所以![]() 為等腰直角三角形,算出
為等腰直角三角形,算出![]() 的直線解析式,
的直線解析式,![]() 的坐標(biāo),從而求解;②同理得到
的坐標(biāo),從而求解;②同理得到![]() 的解析式和
的解析式和![]() 的坐標(biāo),
的坐標(biāo),![]() 為等腰直角三角形,算出
為等腰直角三角形,算出![]() 的解析式,從而求解.
的解析式,從而求解.
解:(1)![]()
![]()
![]()
(2)![]()
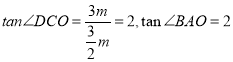
![]()
![]()
![]()
![]()
![]()
分別作![]() ,
,
![]()
設(shè)![]()
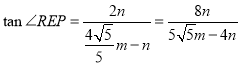
![]()
可證![]()
設(shè)![]()
![]()
作![]()
![]()
![]()
解![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() .
.
(3)過(guò)K作![]() 軸,過(guò)E作
軸,過(guò)E作![]() ,
,
由(1)得![]() ,
,
![]()
由(2)![]()
![]()
![]()
情況1,設(shè)K![]() ,M型可證
,M型可證![]() ,
,
![]() ,
,
![]()
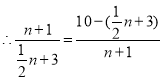
解得:![]()
所以![]() 為等腰直角三角形
為等腰直角三角形
直線KP的解析式為![]() ,
,
直線AB的解析式為![]()
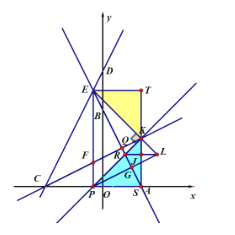
情況2,同理得到KP的解析式為![]() ,
,
直線AB的解析式為![]() ,
,
![]() 為等腰直角三角形
為等腰直角三角形
直線EK的解析式為![]()
直線PG的解析式為![]() ,
,
![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,對(duì)于兩個(gè)點(diǎn)
中,對(duì)于兩個(gè)點(diǎn)![]() ,
,![]() 和圖形
和圖形![]() ,如果在圖形上存在點(diǎn)
,如果在圖形上存在點(diǎn)![]() ,
,![]() (
(![]() ,
,![]() 可以重合),使得
可以重合),使得![]() ,那么稱(chēng)點(diǎn)
,那么稱(chēng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 是圖形
是圖形![]() 的一對(duì)“倍點(diǎn)”.已知⊙O的半徑為
的一對(duì)“倍點(diǎn)”.已知⊙O的半徑為![]() ,點(diǎn)
,點(diǎn)![]() .
.
(1)①點(diǎn)![]() 到⊙O的最大值是_______,最小值是_______;
到⊙O的最大值是_______,最小值是_______;
②在![]() ,
,![]() ,這兩個(gè)點(diǎn)中,與點(diǎn)
,這兩個(gè)點(diǎn)中,與點(diǎn)![]() 是⊙O的一對(duì)“倍點(diǎn)”的是_______;
是⊙O的一對(duì)“倍點(diǎn)”的是_______;
(2)在直線![]() 上存在點(diǎn)
上存在點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 是⊙O的一對(duì)“倍點(diǎn)”,求
是⊙O的一對(duì)“倍點(diǎn)”,求![]() 的取值范圍;
的取值范圍;
(3)已知直線![]() ,與
,與![]() 軸、
軸、![]() 軸分別交于點(diǎn)的
軸分別交于點(diǎn)的![]() ,
,![]() ,若線段
,若線段![]() (含端點(diǎn)
(含端點(diǎn)![]() ,
,![]() )上所有點(diǎn)與點(diǎn)
)上所有點(diǎn)與點(diǎn)![]() 都是⊙O的一對(duì)“倍點(diǎn)”,直接寫(xiě)出
都是⊙O的一對(duì)“倍點(diǎn)”,直接寫(xiě)出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)二次函數(shù)y=(ax-1)(x-a),其中a是常數(shù),且a≠0.
(1)當(dāng)a=2時(shí),試判斷點(diǎn)(-![]() ,-5)是否在該函數(shù)圖象上.
,-5)是否在該函數(shù)圖象上.
(2)若函數(shù)的圖象經(jīng)過(guò)點(diǎn)(1,-4),求該函數(shù)的表達(dá)式.
(3)當(dāng)![]() -1≤x≤
-1≤x≤![]() +1時(shí),y隨x的增大而減小,求a的取值范圍.
+1時(shí),y隨x的增大而減小,求a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
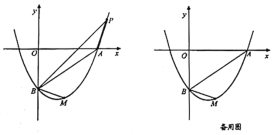
【題目】若二次函數(shù)![]() 的圖象與
的圖象與![]() 軸分別交于點(diǎn)
軸分別交于點(diǎn)![]() 、
、![]() ,且過(guò)點(diǎn)
,且過(guò)點(diǎn)![]() .
.
(1)求二次函數(shù)表達(dá)式;
(2)若點(diǎn)![]() 為拋物線上第一象限內(nèi)的點(diǎn),且
為拋物線上第一象限內(nèi)的點(diǎn),且![]() ,求點(diǎn)
,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)在拋物線上(![]() 下方)是否存在點(diǎn)
下方)是否存在點(diǎn)![]() ,使
,使![]() ?若存在,求出點(diǎn)
?若存在,求出點(diǎn)![]() 到
到![]() 軸的距離;若不存在,請(qǐng)說(shuō)明理由.
軸的距離;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
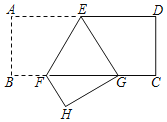
【題目】如圖,矩形ABCD中,點(diǎn)E,F分別在AD,BC上,且AE=DE,BC=3BF,連接EF,將矩形ABCD沿EF折疊,點(diǎn)A恰好落在BC邊上的點(diǎn)G處,則cos∠EGF的值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
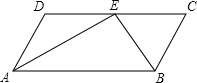
【題目】已知:如圖,在四邊形ABCD中,AD∥BC.點(diǎn)E為CD邊上一點(diǎn),AE與BE分別為∠DAB和∠CBA的平分線.
(1)請(qǐng)你添加一個(gè)適當(dāng)?shù)臈l件 ,使得四邊形ABCD是平行四邊形,并證明你的結(jié)論;
(2)作線段AB的垂直平分線交AB于點(diǎn)O,并以AB為直徑作⊙O(要求:尺規(guī)作圖,保留作圖痕跡,不寫(xiě)作法);
(3)在(2)的條件下,⊙O交邊AD于點(diǎn)F,連接BF,交AE于點(diǎn)G,若AE=4,sin∠AGF=![]() ,求⊙O的半徑.
,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,線段
,線段![]() 上一動(dòng)點(diǎn)
上一動(dòng)點(diǎn)![]() ,以
,以![]() 的速度從點(diǎn)
的速度從點(diǎn)![]() 出發(fā)向終點(diǎn)
出發(fā)向終點(diǎn)![]() 運(yùn)動(dòng).過(guò)點(diǎn)
運(yùn)動(dòng).過(guò)點(diǎn)![]() 作
作![]() ,交折線
,交折線![]() 于點(diǎn)
于點(diǎn)![]() ,以
,以![]() 為一邊,在
為一邊,在![]() 左側(cè)作正方形
左側(cè)作正方形![]() .設(shè)運(yùn)動(dòng)時(shí)間為
.設(shè)運(yùn)動(dòng)時(shí)間為![]()
![]() ,正方形
,正方形![]() 與
與![]() 重疊部分面積為
重疊部分面積為![]() .
.
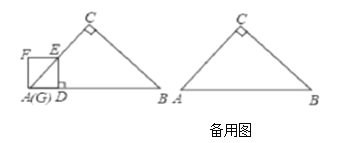
(1)![]() ________
________![]() ;
;
(2)當(dāng)![]() 為何值時(shí),點(diǎn)
為何值時(shí),點(diǎn)![]() 在
在![]() 上;
上;
(3)求![]() 與
與![]() 之間的函數(shù)關(guān)系式,并寫(xiě)出自變量
之間的函數(shù)關(guān)系式,并寫(xiě)出自變量![]() 的取值范圍;
的取值范圍;
(4)直線![]() 將
將![]() 面積分成
面積分成![]() 兩部分時(shí),直接寫(xiě)出
兩部分時(shí),直接寫(xiě)出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】一個(gè)不透明箱子中有2個(gè)紅球,1個(gè)黑球和1個(gè)白球,四個(gè)小球的形狀、大小完全相同.
(1)從中隨機(jī)摸取1個(gè)球,則摸到黑球的概率為 ;
(2)小明和小貝做摸球游戲,游戲規(guī)則如下.

你認(rèn)為這個(gè)游戲公平嗎?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某考察船在某海域進(jìn)行科考活動(dòng),在點(diǎn)A測(cè)得小島C在它的東北方向上,它沿南偏東37°方向航行了2海里到達(dá)點(diǎn)B處,又測(cè)得小島C在它的北偏東23°方向上.
(1)求∠C的度數(shù);
(2)求該考察船在點(diǎn)B處與小島C之間的距離.(精確到0.1海里)
(參考數(shù)據(jù):sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
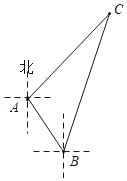
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com