
【題目】如圖,拋物線![]() :
:![]() (
(![]() ,
,![]() 是常數(shù))經(jīng)過
是常數(shù))經(jīng)過![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
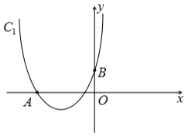
(1)求![]() ,
,![]() 的值;
的值;
(2)向右平移拋物線![]() ,使它經(jīng)過點(diǎn)
,使它經(jīng)過點(diǎn)![]() ,得拋物線
,得拋物線![]() ,
,![]() 與
與![]() 軸的一個(gè)交點(diǎn)為
軸的一個(gè)交點(diǎn)為![]() ,且在另一個(gè)交點(diǎn)的左側(cè).
,且在另一個(gè)交點(diǎn)的左側(cè).
①求拋物線![]() 的表達(dá)式;
的表達(dá)式;
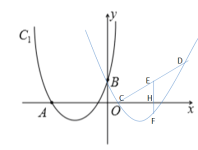
②![]() 是點(diǎn)
是點(diǎn)![]() 關(guān)于拋物線
關(guān)于拋物線![]() 對(duì)稱軸的對(duì)稱點(diǎn),
對(duì)稱軸的對(duì)稱點(diǎn),![]() 是線段
是線段![]() 上一點(diǎn),
上一點(diǎn),![]() 軸,交拋物線
軸,交拋物線![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 為垂足,設(shè)
為垂足,設(shè)![]() ,線段
,線段![]() 的長(zhǎng)為
的長(zhǎng)為![]() ,求
,求![]() 的值,使
的值,使![]() 取得最大值.
取得最大值.
【答案】(1)![]() ,2;(2)①
,2;(2)①![]() ,②3
,②3
【解析】
(1)將A、B兩點(diǎn)坐標(biāo)代入![]() 即可求出
即可求出![]() ,
,![]() 的值.
的值.
(2)將(1)中求得的拋物線![]() 的解析式
的解析式![]() 化為頂點(diǎn)式,根據(jù)
化為頂點(diǎn)式,根據(jù)![]() 和
和![]() 關(guān)于
關(guān)于![]() 軸軸對(duì)稱,即可求得
軸軸對(duì)稱,即可求得![]() 解析式.
解析式.
②先求出![]() 關(guān)于直線
關(guān)于直線![]() 的對(duì)稱點(diǎn)
的對(duì)稱點(diǎn)![]() ,顯然
,顯然![]() ,求出直線
,求出直線![]() 的解析式為
的解析式為![]() ,設(shè)
,設(shè)![]() ,
,![]() ,再根據(jù)
,再根據(jù)![]() ,得出
,得出![]() ,即可求解.
,即可求解.
(1)∵![]() ,
,![]()
∴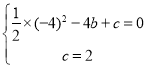
解得![]()
故答案為:![]() ,
,![]()
(2)①由(1)得拋物線![]() 的解析式為
的解析式為![]()
![]() 和
和![]() 關(guān)于
關(guān)于![]() 軸軸對(duì)稱,則
軸軸對(duì)稱,則![]() :
:![]()
∴![]() 即為所求.
即為所求.
②∵![]() 關(guān)于直線
關(guān)于直線![]() 的對(duì)稱點(diǎn)為
的對(duì)稱點(diǎn)為![]()
顯然![]()
∵![]() ,
,![]()
∴直線![]() 的解析式為
的解析式為![]()
∵點(diǎn)![]() 在線段
在線段![]() 上
上
∴![]()
∵點(diǎn)![]() 在拋物線
在拋物線![]() 上
上
∴![]()
令![]() ,得
,得![]()
∴當(dāng)![]() 時(shí),
時(shí),![]() 取得最大值2
取得最大值2
故答案為:![]() ;當(dāng)
;當(dāng)![]() 時(shí),
時(shí),![]() 取得最大值2
取得最大值2



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀下面材料:當(dāng)前,中國(guó)互聯(lián)網(wǎng)產(chǎn)業(yè)發(fā)展迅速,互聯(lián)網(wǎng)教育市場(chǎng)增長(zhǎng)率位居全行業(yè)前列.以下是根據(jù)某媒體發(fā)布的2012﹣2015年互聯(lián)網(wǎng)教育市場(chǎng)規(guī)模的相關(guān)數(shù)據(jù),繪制的統(tǒng)計(jì)圖表的一部分.
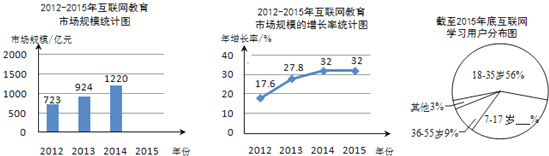
(1)2015年互聯(lián)網(wǎng)教育市場(chǎng)規(guī)模約是 億元(結(jié)果精確到1億元),并補(bǔ)全條形統(tǒng)計(jì)圖;
(2)截至2015年底,約有5億網(wǎng)民使用互聯(lián)網(wǎng)進(jìn)行學(xué)習(xí),互聯(lián)網(wǎng)學(xué)習(xí)用戶的年齡分布如圖所示,請(qǐng)你補(bǔ)全扇形統(tǒng)計(jì)圖,并估計(jì)7﹣17歲年齡段有 億網(wǎng)民通過互聯(lián)網(wǎng)進(jìn)行學(xué)習(xí);
(3)根據(jù)以上材料,寫出你的思考、感受或建議(一條即可).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
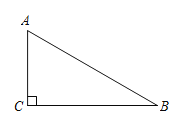
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 邊上一點(diǎn),沿直線
邊上一點(diǎn),沿直線![]() 翻折
翻折![]() ,點(diǎn)
,點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,如果
處,如果![]() ,那么
,那么![]() 的長(zhǎng)為__________.
的長(zhǎng)為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,點(diǎn)O在BC上,以線段OC的長(zhǎng)為半徑的⊙O與AB相切于點(diǎn)D,分別交BC、AC于點(diǎn)E、F,連接ED并延長(zhǎng),交CA的延長(zhǎng)線于點(diǎn)G.
(1)求證:∠DOC=2∠G.
(2)已知⊙O的半徑為3.
①若BE=2,則DA= .
②當(dāng)BE= 時(shí),四邊形DOCF為菱形.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() (
(![]() ,
,![]() 是常數(shù)),其圖象與水平直線
是常數(shù)),其圖象與水平直線![]() ,
,![]() ,鉛直直線
,鉛直直線![]() ,
,![]() 的位置如圖所示,若以其中的兩條直線為
的位置如圖所示,若以其中的兩條直線為![]() 軸,
軸,![]() 軸所在的直線建立平面直角坐標(biāo)系(向右為
軸所在的直線建立平面直角坐標(biāo)系(向右為![]() 軸正方向,向上為
軸正方向,向上為![]() 軸正方向),則下列說法正確的是( )
軸正方向),則下列說法正確的是( )

A.![]() 軸、
軸、![]() 軸所在直線可以是直線
軸所在直線可以是直線![]() 和直線
和直線![]() B.
B.![]() 軸、
軸、![]() 軸所在直線可以是直線
軸所在直線可以是直線![]() 和直線
和直線![]()
C.![]() 軸、
軸、![]() 軸所在直線可以是直線
軸所在直線可以是直線![]() 和直線
和直線![]() D.
D.![]() 軸、
軸、![]() 軸所在直線可以是直線
軸所在直線可以是直線![]() 和直線
和直線![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
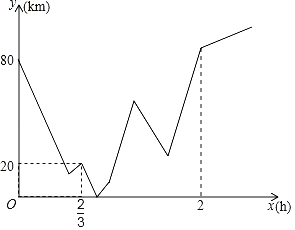
【題目】A、B兩地之間有一修理廠C,一日小海和王陸分別從A、B兩地同時(shí)出發(fā)相向而行,王陸開車,小海騎摩托.二人相遇時(shí)小海的摩托車突然出故障無法前行,王陸決定將小海和摩托車一起送回到修理廠C后再繼續(xù)按原路前行,王陸到達(dá)A地后立即返回B地,到B地后不再繼續(xù)前行,等待小海前來(裝載摩托車時(shí)間和掉頭時(shí)間忽略不計(jì)),整個(gè)行駛過程中王陸速度不變,而小海在修理廠花了十分鐘修好摩托車,為了趕時(shí)間,提速![]() 前往目的地B,小海到達(dá)B地后也結(jié)束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時(shí)間之間x(h)的關(guān)系,則當(dāng)王陸第二次與小海在行駛中相遇時(shí),小海離目的地B還有_____km.
前往目的地B,小海到達(dá)B地后也結(jié)束行程,若圖象表示的是小海與王陸二人到修理廠C的距離和y(km)與小海出行時(shí)間之間x(h)的關(guān)系,則當(dāng)王陸第二次與小海在行駛中相遇時(shí),小海離目的地B還有_____km.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1和圖2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如圖1,AH⊥BC于點(diǎn)H,則AH=___,AC=___,△ABC的面積![]() =___.
=___.
拓展:如圖2,點(diǎn)D在AC上(可與點(diǎn)A、C重合),分別過點(diǎn)A、C作直線BD的垂線,垂足為E、F,設(shè)BD=x,AE=m,CF=n,(當(dāng)點(diǎn)D與A重合時(shí),我們認(rèn)為![]() =0).
=0).
(1)用含x、m或n的代數(shù)式表示![]() 及
及![]() ;
;
(2)求(m+n)與x的函數(shù)關(guān)系式,并求(m+n)的最大值和最小值;
(3)對(duì)給定的一個(gè)x值,有時(shí)只能確定唯一的點(diǎn)D,指出這樣的x的取值范圍.
發(fā)現(xiàn):請(qǐng)你確定一條直線,使得A、B、C三點(diǎn)到這條直線的距離之和最小(不必寫出過程),并寫出這個(gè)最小值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為提升學(xué)生的藝術(shù)素養(yǎng),某校計(jì)劃開設(shè)四門選修課程:聲樂、舞蹈、書法、攝影.要求每名學(xué)生必須選修且只能選修一門課程,為保證計(jì)劃的有效實(shí)施,學(xué)校隨機(jī)對(duì)部分學(xué)生進(jìn)行了一次調(diào)查,并將調(diào)査結(jié)果繪制成如下不完整的統(tǒng)計(jì)表和統(tǒng)計(jì)圖.
學(xué)生選修課程統(tǒng)計(jì)表
課程 | 人數(shù) | 所占百分比 |
聲樂 | 14 |
|
舞蹈 | 8 |
|
書法 | 16 |
|
攝影 |
|
|
合計(jì) |
|
|

根據(jù)以上信息,解答下列問題:
(1)![]() ,
,![]() .
.
(2)求出![]() 的值并補(bǔ)全條形統(tǒng)計(jì)圖.
的值并補(bǔ)全條形統(tǒng)計(jì)圖.
(3)該校有1500名學(xué)生,請(qǐng)你估計(jì)選修“聲樂”課程的學(xué)生有多少名.
(4)七(1)班和七(2)班各有2人選修“舞蹈”課程且有舞蹈基礎(chǔ),學(xué)校準(zhǔn)備從這4人中隨機(jī)抽取2人編排“舞蹈”在開班儀式上表演,請(qǐng)用列表法或畫樹狀圖的方法求所抽取的2人恰好來自同一個(gè)班級(jí)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
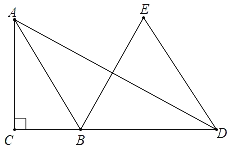
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=![]() ,D是CB延長(zhǎng)線上一點(diǎn),以BD為邊向上作等邊三角形EBD,連接AD,若AD=11,且∠ABE=2∠ADE,則tan∠ADE的值為_____.
,D是CB延長(zhǎng)線上一點(diǎn),以BD為邊向上作等邊三角形EBD,連接AD,若AD=11,且∠ABE=2∠ADE,則tan∠ADE的值為_____.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com