
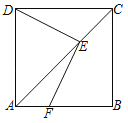
【題目】如圖,正方形ABCD中,AB=3,點(diǎn)E為對(duì)角線AC上一點(diǎn),EF⊥DE交AB于F,若四邊形AFED的面積為4,則四邊形AFED的周長為______.
【答案】4+2![]()
【解析】
連接BE,DF,過E作EN⊥BF于點(diǎn)N,證明△DCE≌△BCE和△BEF為等腰三角形,設(shè)AF=x,用x表示DE與EF,由根據(jù)四邊形ADEF的面積為4,列出x的方程求得x,進(jìn)而求得四邊形ADEF的周長.
解:如圖,連接BE,DF,過E作EN⊥BF于點(diǎn)N,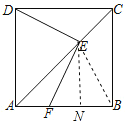
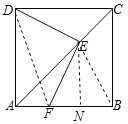
∵四邊形ABCD為正方形,
∴CB=CD,∠BCE=∠DCE=45°,
在△BEC和△DEC中,
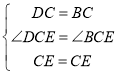 ,
,
∴△DCE≌△BCE(SAS),
∴DE=BE,∠CDE=∠CBE,
∴∠ADE=∠ABE,
∵∠DAB=90°,∠DEF=90°,
∴∠ADE+∠AFE=180°,
∵∠AFE+∠EFB=180°,
∴∠ADE=∠EFB,
∴∠ABE=∠EFB,
∴EF=BE,
∴DE=EF,
設(shè)AF=x,則BF=3-x,
∴FN=BN=![]() BF=
BF=![]() ,
,
∴AN=AF+FN=![]() ,
,
∵∠BAC=∠DAC=45°,∠ANF=90°,
∴EN=AN=![]() ,
,
∴DE=EF=![]() ,
,
∵四邊形AFED的面積為4,
∴S△ADF+S△DEF=4,
∴![]() ×3x+
×3x+![]() ×
×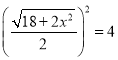 ,
,
解得,x=-7(舍去),或x=1,
∴AF=1,DE=EF=![]() ,
,
∴四邊形AFED的周長為:3+1+![]() +
+![]() =4+
=4+![]() ,
,
故答案為:4+![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的動(dòng)點(diǎn),且
上的動(dòng)點(diǎn),且![]() ,點(diǎn)
,點(diǎn)![]() 關(guān)于
關(guān)于![]() 的對(duì)稱點(diǎn)
的對(duì)稱點(diǎn)![]() 恰好落在
恰好落在![]() 的內(nèi)角平分線上,則
的內(nèi)角平分線上,則![]() 長為_______________.
長為_______________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)著作(九章算術(shù))中有如下問題:“今有人持金出五關(guān),前關(guān)二而稅一.次關(guān)三而稅一,次關(guān)四而稅一,次關(guān)五而稅一,次關(guān)六而稅一,并五關(guān)所稅,適重一斤.”其意思為“今有人持金出五關(guān),第![]() 關(guān)所收稅金為持金的
關(guān)所收稅金為持金的![]() ,第
,第![]() 關(guān)所收稅金為剩余金的
關(guān)所收稅金為剩余金的![]() ,第
,第![]() 關(guān)所收稅金為剩余金的
關(guān)所收稅金為剩余金的![]() ,第
,第![]() 關(guān)所收稅金為剩余金的
關(guān)所收稅金為剩余金的![]() ,第
,第![]() 關(guān)所收稅金為剩余金的
關(guān)所收稅金為剩余金的![]() ,
,![]() 關(guān)所收稅金之和,恰好重
關(guān)所收稅金之和,恰好重![]() 斤.”若設(shè)這個(gè)人原本持金
斤.”若設(shè)這個(gè)人原本持金![]() 斤,根據(jù)題意可列方程為__________ .
斤,根據(jù)題意可列方程為__________ .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,AB∥CD,點(diǎn)E是直線AB上的點(diǎn),過點(diǎn)E的直線l交直線CD于點(diǎn)F,EG平分∠BEF交CD于點(diǎn)G.在直線l繞點(diǎn)E旋轉(zhuǎn)的過程中,圖中∠1,∠2的度數(shù)可以分別是( )
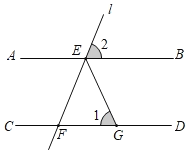
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,折疊矩形![]() ,具體操作:①點(diǎn)
,具體操作:①點(diǎn)![]() 為
為![]() 邊上一點(diǎn)(不與
邊上一點(diǎn)(不與![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直線折疊,
所在的直線折疊,![]() 點(diǎn)的對(duì)稱點(diǎn)為
點(diǎn)的對(duì)稱點(diǎn)為![]() 點(diǎn);②過點(diǎn)
點(diǎn);②過點(diǎn)![]() 對(duì)折
對(duì)折![]() ,折痕
,折痕![]() 所在的直線交
所在的直線交![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() 點(diǎn)的對(duì)稱點(diǎn)為
點(diǎn)的對(duì)稱點(diǎn)為![]() 點(diǎn).
點(diǎn).
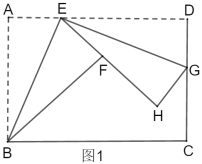
(1)求證:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①點(diǎn)![]() 在移動(dòng)的過程中,求
在移動(dòng)的過程中,求![]() 的最大值.
的最大值.
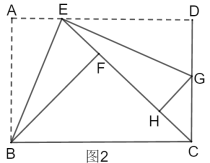
②如圖2,若點(diǎn)![]() 恰在直線
恰在直線![]() 上,連接
上,連接![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于點(diǎn)A,將點(diǎn)A向右平移2個(gè)單位長度,得到點(diǎn)B,點(diǎn)B在拋物線上.
軸交于點(diǎn)A,將點(diǎn)A向右平移2個(gè)單位長度,得到點(diǎn)B,點(diǎn)B在拋物線上.
(1)求點(diǎn)B的坐標(biāo)(用含![]() 的式子表示);
的式子表示);
(2)求拋物線的對(duì)稱軸;
(3)已知點(diǎn)![]() ,
,![]() .若拋物線與線段PQ恰有一個(gè)公共點(diǎn),結(jié)合函數(shù)圖象,求
.若拋物線與線段PQ恰有一個(gè)公共點(diǎn),結(jié)合函數(shù)圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的網(wǎng)格中,有兩個(gè)完全相同的直角三角形紙片,如果把其中一個(gè)三角形紙片先橫向平移![]() 格,再縱向平移
格,再縱向平移![]() 格,就能使它的一條邊與另一個(gè)三角形紙片的一條邊重合,拼接成一個(gè)四邊形,那么
格,就能使它的一條邊與另一個(gè)三角形紙片的一條邊重合,拼接成一個(gè)四邊形,那么![]() 的結(jié)果( )
的結(jié)果( )

A.只有一個(gè)確定的值B.有兩個(gè)不同的值
C.有三個(gè)不同的值D.有三個(gè)以上不同的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:
數(shù)學(xué)活動(dòng)課上,李老師給出如下定義:如果一個(gè)三角形有一邊上的中線等于這條邊的一半,那么稱這個(gè)三角形為“智慧三角形”.
理解:
(1)如圖,已知![]() 、
、![]() 是
是![]() 上兩點(diǎn),請(qǐng)?jiān)趫A上找出滿足條件的點(diǎn)
上兩點(diǎn),請(qǐng)?jiān)趫A上找出滿足條件的點(diǎn)![]() ,使
,使![]() 為“智慧三角形”(畫出點(diǎn)
為“智慧三角形”(畫出點(diǎn)![]() 的位置,保留作圖痕跡);
的位置,保留作圖痕跡);
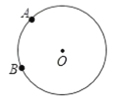
(2)如圖,在正方形![]() 中,
中,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是
是![]() 上一點(diǎn),且
上一點(diǎn),且![]() ,試判斷
,試判斷![]() 是否為“智慧三角形”,并說明理由;
是否為“智慧三角形”,并說明理由;
運(yùn)用:
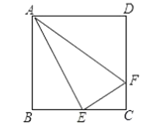
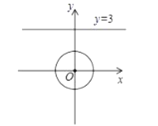
(3)如圖,在平面直角坐標(biāo)系![]() 中,
中,![]() 的半徑為1,點(diǎn)
的半徑為1,點(diǎn)![]() 是直線
是直線![]() 上的一點(diǎn),若在
上的一點(diǎn),若在![]() 上存在一點(diǎn)
上存在一點(diǎn)![]() ,使得
,使得![]() 為“智慧三角形”,當(dāng)其面積取得最小值時(shí),直接寫出此時(shí)點(diǎn)
為“智慧三角形”,當(dāng)其面積取得最小值時(shí),直接寫出此時(shí)點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明和小亮一起玩摸棋子的游戲.在一個(gè)密閉不透明的盒子中裝有2枚白色棋子和2枚黑色棋子,棋子除顏色外其余均相同.從這個(gè)盒子中隨機(jī)摸出1枚棋子記下顏色,放回;搖勻后,再隨機(jī)地摸出1枚棋子,并記下顏色,若兩次摸出的棋子顏色相同,則小明勝;若兩次摸出的棋子顏色不相同,則小亮勝.這個(gè)游戲?qū)﹄p方公平嗎?請(qǐng)用畫樹狀圖或列表格的方法說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com