
【題目】如圖,已知在正方形ABCD中,F是CD邊上一點(不與C、D重合),過點D作DG⊥BF交BF延長線于點G.連接AG,交BD于點E,交CD于點M,連接EF.若DG=4,AG=![]() ,則EF的長為____________.
,則EF的長為____________.

【答案】![]()
【解析】試題分析:
如圖作AH⊥BG于H交BC于T,AN⊥GD于N,取BD的中點O,連接OA、OG.
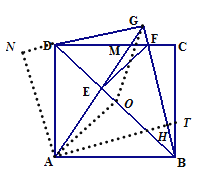
∴∠BAD=∠BGD=90°,
∴OA=OD=OB=OG,
∴A、B、G、D四點共圓,
∴∠AGB=∠ADB=45°,∠AGD=∠ABD=45°,
∴AH=GH,AN=NG,
∵∠N=∠AHG=∠HGN=90°,
∴四邊形ANGH是矩形,∵AH=HG,
∴四邊形ANGH是正方形,
∵AG=![]() ,
,
∴AH=HG=GN=AN=5,
易證△AND≌△AHB,
∴DN=BH,
∴GD+GB=GN-DN+GH+BH=2GN=10,
∴4+GB=10,
∴GB=6,BD=![]() =
=![]() =
=![]() ,
,
∴BH=1,
∵△BHT∽△AHB,
∴BH2=AHHT,
∴HT=![]() ,
,
∴AT=AH+TH=![]() ,
,
易證△ABT≌△BCF,
∴AT=BF=![]() ,
,
∵△BEF∽△BGD,
∴![]() ,
,
∴ ,
,
∴EF=![]() .
.
故答案為![]() .
.


科目:初中數學 來源: 題型:
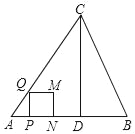
【題目】如圖,在△ABC中,AB=AC=5,AB邊上的高CD=4,點P從點A出發,沿AB以每秒3個單位長度的速度向終點B運動,當點P不與點A、B重合時,過點P作PQ⊥AB,交邊AC或邊BC于點Q,以PQ為邊向右側作正方形PQMN.設正方形PQMN與△ABC重疊部分圖形的面積為S(平方單位),點P運動的時間為t(秒).
(1)直接寫出tanB的值為 .
(2)求點M落在邊BC上時t的值.
(3)當正方形PQMN與△ABC重疊部分為四邊形時,求S與t之間的函數關系式.
(4)邊BC將正方形PQMN的面積分為1:3兩部分時,直接寫出t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以ABCD 的四條邊為邊,分別向外作正方形,連結 EF,GH,IJ,KL.如果ABCD 的 面積為 8,則圖中陰影部分四個三角形的面積和為( )

A.8B.12C.16D.20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著網絡的發展,我們的生活越來越方便,越來越多的人在網絡上購物,微商這個行業也悄然興起,很多人通過微信平臺銷售商品.
(1)某水果微商今年九月購進榴蓮和奇異果共1000千克,它們的進價均為每千克24 元,然后以榴蓮售價每千克45元,奇異果售價每千克36元的價格很快銷售完,若該水果微商九月獲利不低于17400元,求應購進榴蓮至少多少千克?
(2)為了增加銷售量,獲得更大的利潤,在進價不變的情況下,該水果微商十月決定調整售價,榴蓮的售價在九月的基礎上下調![]() (降價后的售價不低于進價),奇異果的售價在九月的基礎上上漲
(降價后的售價不低于進價),奇異果的售價在九月的基礎上上漲![]() ,同時,與(1)中獲得的最低利潤時的銷售量相比,榴蓮的銷售量下降了
,同時,與(1)中獲得的最低利潤時的銷售量相比,榴蓮的銷售量下降了![]() ,而奇異果的銷售量上升了
,而奇異果的銷售量上升了![]() ,結果十月的銷售額比九月增加了600元.求
,結果十月的銷售額比九月增加了600元.求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D. 下列結論:①AD是∠BAC的平分線;②點D在AB的垂直平分線上;③∠ADC=60°;④
MN的長為半徑畫弧,兩弧交于點P,連結AP并延長交BC于點D. 下列結論:①AD是∠BAC的平分線;②點D在AB的垂直平分線上;③∠ADC=60°;④![]() 。其中正確的結論有( )
。其中正確的結論有( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在東營市中小學標準化建設工程中,某學校計劃購進一批電腦和電子白板,經過市場考察得知,購買1臺電腦和2臺電子白板需要3.5萬元,購買2臺電腦和1臺電子白板需要2.5萬元.
(1)求每臺電腦、每臺電子白板各多少萬元?
(2)根據學校實際,需購進電腦和電子白板共30臺,總費用不超過30萬元,但不低于28萬元,請你通過計算求出有幾種購買方案,哪種方案費用最低.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A、B兩地相距4800米,甲從A地出發步行到B地,20分鐘后乙從B地出發騎自行車到A地,設甲步行的時間為x分鐘,甲、乙兩人離A地的距離分別為![]() 米、
米、![]() 米,
米,![]() 、
、![]() 與x的函數關系圖象如圖所示,根據圖象解答下列問題:
與x的函數關系圖象如圖所示,根據圖象解答下列問題:

(1)直接寫出y![]() 、y
、y![]() 與x的函數關系式,并寫出自變量x的取值范圍;
與x的函數關系式,并寫出自變量x的取值范圍;
(2)求甲出發后多少分鐘兩人相遇,相遇時乙離A地多少米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com