
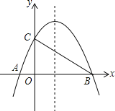
【題目】如圖,已知拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸相交于點(diǎn)
軸相交于點(diǎn)![]() .若已知
.若已知![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() .點(diǎn)
.點(diǎn)![]() 在拋物線的對稱軸上,當(dāng)
在拋物線的對稱軸上,當(dāng)![]() 為等腰三角形時,點(diǎn)
為等腰三角形時,點(diǎn)![]() 的坐標(biāo)為________.
的坐標(biāo)為________.
【答案】![]() ,
,![]() ,
,![]()
【解析】
首先求出拋物線解析式,然后利用配方法或利用公式x=-![]() 求出對稱軸方程,由此可設(shè)可設(shè)點(diǎn)Q(3,t),若△ACQ為等腰三角形,則有三種可能的情形,需要分類討論,逐一計算,避免漏解.
求出對稱軸方程,由此可設(shè)可設(shè)點(diǎn)Q(3,t),若△ACQ為等腰三角形,則有三種可能的情形,需要分類討論,逐一計算,避免漏解.
∵拋物線y=-![]() x2+bx+4的圖象經(jīng)過點(diǎn)A(-2,0),
x2+bx+4的圖象經(jīng)過點(diǎn)A(-2,0),
∴-![]() ×(-2)2+b×(-2)+4=0,
×(-2)2+b×(-2)+4=0,
解得:b=![]() ,
,
∴拋物線解析式為 y=-![]() x2+
x2+![]() x+4,
x+4,
又∵y=-![]() x2+
x2+![]() x+4=-
x+4=-![]() (x-3)2+
(x-3)2+![]() ,
,
∴對稱軸方程為:x=3,
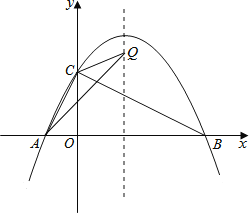
∴可設(shè)點(diǎn)Q(3,t),則可求得:
AC=![]() ,
,
AQ=![]() ,
,
CQ=![]() .
.
i)當(dāng)AQ=CQ時,
有![]() =
=![]() ,
,
即25+t2=t2-8t+16+9,
解得t=0,
∴Q1(3,0);
ii)當(dāng)AC=AQ時,
有![]() =2
=2![]() ,
,
即t2=-5,此方程無實(shí)數(shù)根,
∴此時△ACQ不能構(gòu)成等腰三角形;
iii)當(dāng)AC=CQ時,
有2![]() =
=![]() ,
,
整理得:t2-8t+5=0,
解得:t=4±![]() ,
,
∴點(diǎn)Q坐標(biāo)為:Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
綜上所述,存在點(diǎn)Q,使△ACQ為等腰三角形,點(diǎn)Q的坐標(biāo)為:Q1(3,0),Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
故答案為:(3,0),(3,4+![]() ),(3,4-
),(3,4-![]() ).
).



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】胖娃、猴子兩人在1800米長的直線道路上跑步,胖娃、猴子兩人同起點(diǎn)、同方向出發(fā),并分別以不同的速度勻速前進(jìn).已知,胖娃出發(fā)30秒后,猴子出發(fā),猴子到終點(diǎn)后立即返回,并以原來的速度前進(jìn),最后與胖娃相遇,此時跑步結(jié)束. 如圖,![]() (米)表示胖娃、猴子兩人之間的距離,x(秒)表示胖娃出發(fā)的時間,圖中折線及數(shù)據(jù)表示整個跑步過程中y與x函數(shù)關(guān)系.那么,猴子到終點(diǎn)后_______秒與胖娃相遇.
(米)表示胖娃、猴子兩人之間的距離,x(秒)表示胖娃出發(fā)的時間,圖中折線及數(shù)據(jù)表示整個跑步過程中y與x函數(shù)關(guān)系.那么,猴子到終點(diǎn)后_______秒與胖娃相遇.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】正方形ABCD的邊長為3,點(diǎn)E,F(xiàn)分別在射線DC,DA上運(yùn)動,且DE=DF.連接BF,作EH⊥BF所在直線于點(diǎn)H,連接CH.
(1)如圖1,若點(diǎn)E是DC的中點(diǎn),CH與AB之間的數(shù)量關(guān)系是 ;
(2)如圖2,當(dāng)點(diǎn)E在DC邊上且不是DC的中點(diǎn)時,(1)中的結(jié)論是否成立?若成立給出證明;若不成立,說明理由;
(3)如圖3,當(dāng)點(diǎn)E,F(xiàn)分別在射線DC,DA上運(yùn)動時,連接DH,過點(diǎn)D作直線DH的垂線,交直線BF于點(diǎn)K,連接CK,請直接寫出線段CK長的最大值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,且當(dāng)
,且當(dāng)![]() 和
和![]() 時二次函數(shù)的函數(shù)值
時二次函數(shù)的函數(shù)值![]() 相等.
相等.
(![]() )求實(shí)數(shù)
)求實(shí)數(shù)![]() 、
、![]() 的值.
的值.
(![]() )如圖
)如圖![]() ,動點(diǎn)
,動點(diǎn)![]() 、
、![]() 同時從
同時從![]() 點(diǎn)出發(fā),其中點(diǎn)
點(diǎn)出發(fā),其中點(diǎn)![]() 以每秒
以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 邊向終點(diǎn)
邊向終點(diǎn)![]() 運(yùn)動,點(diǎn)
運(yùn)動,點(diǎn)![]() 以每秒
以每秒![]() 個單位長度的速度沿射線
個單位長度的速度沿射線![]() 方向運(yùn)動,當(dāng)點(diǎn)
方向運(yùn)動,當(dāng)點(diǎn)![]() 停止運(yùn)動時,點(diǎn)
停止運(yùn)動時,點(diǎn)![]() 隨之停止運(yùn)動.設(shè)運(yùn)動時間為
隨之停止運(yùn)動.設(shè)運(yùn)動時間為![]() 秒.連接
秒.連接![]() ,將
,將![]() 沿
沿![]() 翻折,使點(diǎn)
翻折,使點(diǎn)![]() 落在點(diǎn)
落在點(diǎn)![]() 處,得到
處,得到![]() .
.
①是否存在某一時刻![]() ,使得
,使得![]() 為直角三角形?若存在,求出
為直角三角形?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
②設(shè)![]() 與
與![]() 重疊部分的面積為
重疊部分的面積為![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式.
的函數(shù)關(guān)系式.


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,672可以寫成6×102+7×10+2,對于多項(xiàng)式而言,關(guān)于某一字母的多項(xiàng)式都可以按這個字母的降冪排列比如7x+2+6x2可以寫成6x2+7x+2.在解決多項(xiàng)式相除的問題時,我們通過對比發(fā)現(xiàn),可以類比多位數(shù)的除法,用豎式進(jìn)行計算,例如:(7x+2+6x2)÷(2x+1),仿照672÷21計算如圖,因此:(7x+2+6x2)÷(2x+1)=3x+2.根據(jù)閱讀材料,

(1)試判斷:x3﹣x2﹣5x﹣3能否被x+1整除_____,(請用“能”或“不能”填空)
(2)多項(xiàng)式2x5+3x3+5x2﹣2x+10除以x2+1的商式是_____,余式是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】等邊三角形![]() 的邊長為
的邊長為![]() ,將其放置在如圖所示的平面直角坐標(biāo)系中,其中
,將其放置在如圖所示的平面直角坐標(biāo)系中,其中![]() 邊在
邊在![]() 軸上,
軸上,![]() 邊的高
邊的高![]() 在
在![]() 軸上.一只電子蟲從
軸上.一只電子蟲從![]() 出發(fā),先沿
出發(fā),先沿![]() 軸到達(dá)
軸到達(dá)![]() 點(diǎn),再沿
點(diǎn),再沿![]() 到達(dá)
到達(dá)![]() 點(diǎn),已知電子蟲在
點(diǎn),已知電子蟲在![]() 軸上運(yùn)動的速度是在
軸上運(yùn)動的速度是在![]() 上運(yùn)動速度的
上運(yùn)動速度的![]() 倍,若電子蟲走完全程的時間最短,則點(diǎn)
倍,若電子蟲走完全程的時間最短,則點(diǎn)![]() 的坐標(biāo)為________.
的坐標(biāo)為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列命題中,是假命題的是( )
A.在△ABC中,若∠B=∠C﹣∠A,則△ABC是直角三角形
B.在△ABC中,若a![]() =(b+c) (b﹣c),則△ABC是直角三角形
=(b+c) (b﹣c),則△ABC是直角三角形
C.在△ABC中,若∠A:∠B:∠C=3:4:5,則△ABC是直角三角形
D.在△ABC中,若a:b:c=3:4:5,則△ABC是直角三角形
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】我們知道,在平面內(nèi),如果一個圖形繞著一個定點(diǎn)旋轉(zhuǎn)一定的角度后能與自身重合,那么就稱這個圖形是旋轉(zhuǎn)對稱圖形,轉(zhuǎn)的這個角稱為這個圖形的一個旋轉(zhuǎn)角.例如,正方形繞著它的對角線的交點(diǎn)旋轉(zhuǎn)![]() 后能與自身重合所以正方形是旋轉(zhuǎn)對稱圖形,它有一個旋轉(zhuǎn)角為
后能與自身重合所以正方形是旋轉(zhuǎn)對稱圖形,它有一個旋轉(zhuǎn)角為![]() .
.
![]() 判斷下列說法是否正確(在相應(yīng)橫線里填上“對”或“錯”)
判斷下列說法是否正確(在相應(yīng)橫線里填上“對”或“錯”)
①正五邊形是旋轉(zhuǎn)對稱圖形,它有一個旋轉(zhuǎn)角為![]() .________
.________
②長方形是旋轉(zhuǎn)對稱圖形,它有一個旋轉(zhuǎn)角為![]() .________
.________
![]() 填空:下列圖形中時旋轉(zhuǎn)對稱圖形,且有一個旋轉(zhuǎn)角為
填空:下列圖形中時旋轉(zhuǎn)對稱圖形,且有一個旋轉(zhuǎn)角為![]() 的是________.(寫出所有正確結(jié)論的序號)
的是________.(寫出所有正確結(jié)論的序號)
①正三角形②正方形③正六邊形④正八邊形
![]() 寫出兩個多邊形,它們都是旋轉(zhuǎn)對稱圖形,都有一個旋轉(zhuǎn)角為
寫出兩個多邊形,它們都是旋轉(zhuǎn)對稱圖形,都有一個旋轉(zhuǎn)角為![]() ,其中一個是軸對稱圖形,但不是中心對稱圖形;另一個既是軸對稱圖形,又是中心對稱圖形.
,其中一個是軸對稱圖形,但不是中心對稱圖形;另一個既是軸對稱圖形,又是中心對稱圖形.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com