
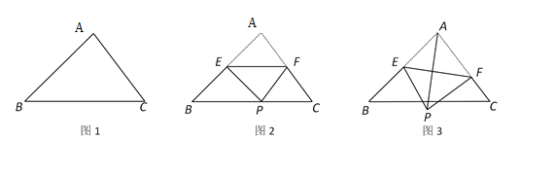
【題目】如圖,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC邊上的高線長.
(2)點E為線段AB的中點,點F在邊AC上,連結EF,沿EF將△AEF折疊得到△PEF.
①如圖2,當點P落在BC上時,求∠AEP的度數.
②如圖3,連結AP,當PF⊥AC時,求AP的長.
【答案】(1)4;(2)①90°;②![]()
【解析】
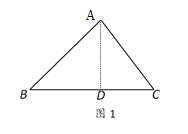
(1)如圖1中,過點A作AD⊥BC于D.解直角三角形求出AD即可.
(2)①證明BE=EP,可得∠EPB=∠B=45°解決問題.
②如圖3中,由(1)可知:AC=![]() ,證明△AEF∽△ACB,推出
,證明△AEF∽△ACB,推出![]() ,由此求出AF即可解決問題.
,由此求出AF即可解決問題.
解:(1)如圖1,過點A作AD⊥BC于點D,
在Rt△ABD中,![]() =
=![]() =4.
=4.
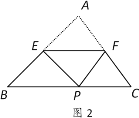
(2)①如圖2,∵△AEF≌△PEF,
∴AE=EP.
又∵AE=BE ,
∴BE=EP,
∴∠EPB=∠B=45°,
∴∠AEP=90°.
②如圖3,由(1)可知:在Rt△ADC中,![]() .
.
∵PF⊥AC,
∴∠PFA=90°.
∵△AEF≌△PEF,
∴∠AFE=∠PFE=45°,則∠AFE=∠B.
又∵∠EAF=∠CAB,
∴△EAF∽△CAB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AF=![]() ,
,
在Rt△AFP中,AF=PF,則AP=![]() =
=![]() .
.



科目:初中數學 來源: 題型:
【題目】觀察以下等式:
第1個等式:23-22=13+2×1+1;
第2個等式:33-32=23+3×2+22;
第3個等式:43-42=33+4×3+32;
……
按照以上規律,解決下列問題:
(1)寫出第4個等式:__________________;
(2)寫出你猜想的第n個等式(用含n的等式表示),并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
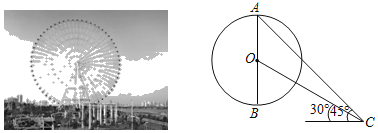
【題目】“南昌之星”摩天輪,位于江西省南昌市紅谷灘新區紅角洲贛江邊上的贛江市民公園,摩天輪高160m(最高點到地面的距離).如圖,點O是摩天輪的圓心,AB是其垂直于地面的直徑,小賢在地面點C處利用測角儀測得摩天輪的最高點A的仰角為45°,測得圓心O的仰角為30°,則摩天輪的半徑為_____m.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列正多邊形中,![]() 是中心,定義:
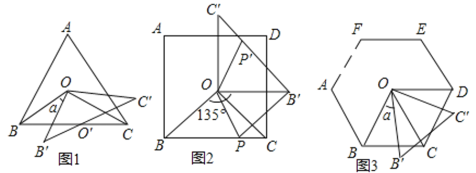
是中心,定義:![]() 為相應正多邊形的基本三角形.如圖1,
為相應正多邊形的基本三角形.如圖1,![]() 是正三角形
是正三角形![]() 的基本三角形;如圖2,
的基本三角形;如圖2,![]() 是正方形
是正方形![]() 的基本三角形;如圖3,
的基本三角形;如圖3,![]() 為正
為正![]() 邊形
邊形![]() …的基本三角形.將基本
…的基本三角形.將基本![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 角度得
角度得![]() .
.
(1)若線段![]() 與線段
與線段![]() 相交點
相交點![]() ,則:
,則:
圖1中![]() 的取值范圍是________;
的取值范圍是________;
圖3中![]() 的取值范圍是________;
的取值范圍是________;
(2)在圖1中,求證![]()
(3)在圖2中,正方形邊長為4,![]() ,邊
,邊![]() 上的一點
上的一點![]() 旋轉后的對應點為
旋轉后的對應點為![]() ,若
,若![]() 有最小值時,求出該最小值及此時
有最小值時,求出該最小值及此時![]() 的長度;
的長度;
(4)如圖3,當![]() 時,直接寫出
時,直接寫出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
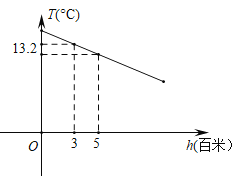
【題目】某地區山峰的高度每增加1百米,氣溫大約降低0.6℃.氣溫T(℃)和高度h(百米)的函數關系如圖所示.請根據圖象解決下列問題:
(1)求高度為5百米時的氣溫.
(2)求T關于h的函數表達式.
(3)測得山頂的氣溫為6℃,求該山峰的高度.
查看答案和解析>>
科目:初中數學 來源: 題型:
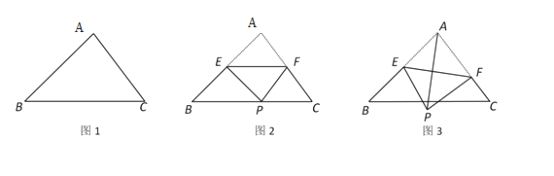
【題目】如圖,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC邊上的高線長.
(2)點E為線段AB的中點,點F在邊AC上,連結EF,沿EF將△AEF折疊得到△PEF.
①如圖2,當點P落在BC上時,求∠AEP的度數.
②如圖3,連結AP,當PF⊥AC時,求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
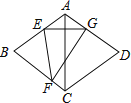
【題目】如圖,已知四邊形ABCD是邊長為6的菱形,且∠BAD=120°,點E,F分別在AB、BC邊上,將菱形沿EF折疊,點B正好落在AD邊的點G處,若EG⊥AC,則FG的長為( )
A.3![]() B.6C.3
B.6C.3![]() D.3
D.3![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=8,BC=6,D為AB邊上的動點,過點D作DE⊥AB交邊AC于點E,過點E作EF⊥DE交BC于點F,連接DF.
(1)當AD=4時,求EF的長度;
(2)求△DEF的面積的最大值;
(3)設O為DF的中點,隨著點D的運動,則點O的運動路徑的長度為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com