
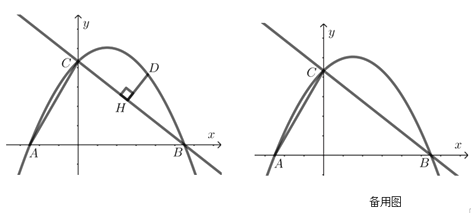
【題目】如圖,在平面直角坐標系中,直線![]() 與x軸交于點B,與y軸交于點C,拋物線
與x軸交于點B,與y軸交于點C,拋物線![]() 經過點B和點C,且與x軸交于另一點A,連接AC,點D在BC上方的拋物線上,設點D的橫坐標為m,過點D作DH⊥BC于點H.
經過點B和點C,且與x軸交于另一點A,連接AC,點D在BC上方的拋物線上,設點D的橫坐標為m,過點D作DH⊥BC于點H.
(1)求拋物線的函數表達式;
(2)線段DH的長為 (用含m的代數式表示);
(3)點M為線段AC上一點,連接OM繞點O順時針旋轉60°得線段ON,連接CN,當CN=![]() ,m=6時,請直接寫出此時線段DM的長.
,m=6時,請直接寫出此時線段DM的長.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用待定系數法即可求得解析式;
(2)利用勾股定理列方程計算即可得出;
(3)作∠NPO=60°(點P在x軸上),作NQ⊥x軸,交x軸于點Q,
作NH⊥y軸交y軸于點H,作MG⊥x軸交x軸于點G,交DS于點T,DS⊥x軸于點S,
做出輔助線后根據條件討論即可.
(1)根據![]() 可得B(11,0),C(0,
可得B(11,0),C(0,![]() ),
),
將B,C兩點代入![]() ,
,
得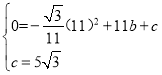 ,解得
,解得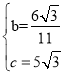 ,
,
∴解析式為:![]() ;
;
(2)由題意可得B(11,0),C(0,![]() ),
),
∴OB=11,OC=![]() ,
,
∵D點的橫坐標為m,
∴D點的坐標可表示為(m,![]() )
)
∴|BC|=![]() ,
,
|DC|=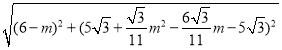 ,
,
|BD|=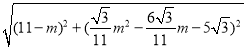 ,
,
設CH=x,
∴|DC|2-x2=|BD|2-(14-x)2
解得x=![]() ,
,
|DH|=![]() ;
;
(3))如圖,作∠NPO=60°(點P在x軸上),作NQ⊥x軸,交x軸于點Q,
作NH⊥y軸交y軸于點H,作MG⊥x軸交x軸于點G,交DS于點T,DS⊥x軸于點S,

∵拋物線![]() 交x軸于點A,B,
交x軸于點A,B,
∴令![]()
解得x1=11,x2=-5,
即A(-5,0),OA=5,
∵tan=![]() ,
,
∴∠CAO=60°,∠ACO=30°,
∵∠MON=60°,∠CAO=120°,
∴∠MOA+∠NOP=120°,∠MOA+∠AMO=120°,
∴∠NOP=∠AMO,
在△MOA和△ONP中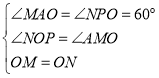 ,
,
∴△MOA≌△ONP(AAS),
∴NP=OA=5,
在Rt△NQP中,QP=NP·cos60°=![]() ,NQ=NP·sin60°=
,NQ=NP·sin60°=![]() ,
,
在四邊形NHOQ中,∠NQO=∠QOP=∠OQN=90°,
∴∠HNQ=90°,
∴四邊形NHOQ是矩形,
∴OH=NQ=![]() ,CH=OC-OH=
,CH=OC-OH=![]() -
-![]() =
=![]() ,
,
在Rt△CHN中,HN=![]() ,
,
在Rt△HNO中,ON=![]() ,
,
∴OM=ON=![]() ,
,
設MG=a,則GC=![]() =
=![]() ,OG=
,OG=![]() -
-![]() ,
,
在Rt△MOG中,DM2=MG2+OG2,
即212=a2+(![]() -
-![]() )2,整理得:(a-3)(2a-9)=0,
)2,整理得:(a-3)(2a-9)=0,
解得a1=3,a2=![]() ,
,
當m=6時,D(6,![]() ),
),
①a1=3時,MT=3+6=9,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△DMT中,DM=![]() ,
,
②a2=![]() 時,MT=
時,MT=![]() +6=
+6=![]() ,TS=OG=
,TS=OG=![]() ,DT=
,DT=![]() -
-![]() =
=![]() ,
,
在Rt△MDT中,DM=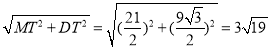 ,
,
綜上DM的值為![]() 或
或![]() .
.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:
【題目】如圖1,已知拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點(
兩點(![]() 點在
點在![]() 點的左側),與
點的左側),與![]() 軸相交于
軸相交于![]() 點,且
點,且![]() .
.

(1)求這條拋物線的解析式;
(2)如圖2,![]() 點在
點在![]() 軸上,且在
軸上,且在![]() 點的右側,
點的右側,![]() 點為拋物線上第二象限內的點,連接
點為拋物線上第二象限內的點,連接![]() 交拋物線于第二象限內的另外一點
交拋物線于第二象限內的另外一點![]() ,點
,點![]() 到
到![]() 軸的距離與點
軸的距離與點![]() 到
到![]() 軸的距離之比為
軸的距離之比為![]() ,已知
,已知![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)如圖3,在(2)的條件下,點![]() 由
由![]() 出發,沿
出發,沿![]() 軸負方向運動,連接
軸負方向運動,連接![]() ,點
,點![]() 在線段
在線段![]() 上,連接
上,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() ,與拋物線相交于點
,與拋物線相交于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一條直線把一個平面圖形分成面積相等的兩部分,那么這條直線叫做該平面圖形的“和諧線”,其“和諧線”被該平面圖形截得的線段叫做該平面圖形的“和諧線段”(例如圓的直徑就是圓的“和諧線段”)
問題探究:
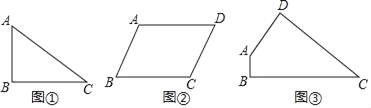
(1)如圖①,已知△ABC中,AB=6,BC=8,∠B=90°,請寫出△ABC的兩條“和諧線段”的長.
(2)如圖②,平行四邊形ABCD中,AB=6,BC=8,∠B=60°,請直接寫出該平行四邊形ABCD的“和諧線段”長的最大值和最小值;
問題解決
(3)如圖③,四邊形ABCD是某市規劃中的商業區示意圖,其中AB=2,CD=10,∠A=135°,∠B=90°,tanC=![]() ,現計劃在商業區內修一條筆直的單行道MN(小道的寬度不計),入口M在BC上,出口N在CD上,使得MN為四邊形ABCD“和諧線段”,在道路一側△MNC區域規劃為公園,為了美觀要求△MNC是以CM為腰的等腰三角形,請通過計算說明設計師的想法能否實現?若可以,請確定點M的位置(即求CM的長).
,現計劃在商業區內修一條筆直的單行道MN(小道的寬度不計),入口M在BC上,出口N在CD上,使得MN為四邊形ABCD“和諧線段”,在道路一側△MNC區域規劃為公園,為了美觀要求△MNC是以CM為腰的等腰三角形,請通過計算說明設計師的想法能否實現?若可以,請確定點M的位置(即求CM的長).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,其對稱軸為直線
點,其對稱軸為直線![]() .
.
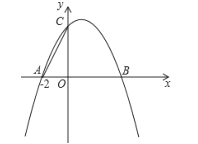
(1)直接寫出拋物線的解析式;
(2)把線段![]() 沿
沿![]() 軸向右平移,設平移后
軸向右平移,設平移后![]() 、
、![]() 的對應點分別為
的對應點分別為![]() 、
、![]() ,當
,當![]() 落在拋物線上時,求
落在拋物線上時,求![]() 、
、![]() 的坐標;
的坐標;
(3)除(2)中的平行四邊形![]() 外,在
外,在![]() 軸和拋物線上是否還分別存在點
軸和拋物線上是否還分別存在點![]() 、
、![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,求出
為頂點的四邊形為平行四邊形?若存在,求出![]() 、
、![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,點E和點F是對角線AC上的兩點,AF=CE,DF=BE,且DF∥BE,過點C作CG⊥AB交AB延長線與點G.
(1)求證:四邊形ABCD是平行四邊形;
(2)若tan∠CAB=![]() ,∠CBG=45°,BC=
,∠CBG=45°,BC=![]() ,則ABCD的面積是 .
,則ABCD的面積是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,點
,點![]() 、
、![]() 是反比例函數
是反比例函數![]()
![]() 圖象上的點,
圖象上的點,![]() 于點
于點![]() ,
,![]() .
.
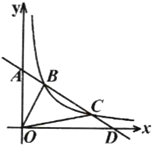
(1)求直線![]() 的函數解析式及反比例函數的解析式;
的函數解析式及反比例函數的解析式;
(2)若![]() 、
、![]() 、
、![]() 的面積分別為
的面積分別為![]() ,
,![]() ,
,![]() ,直接寫出
,直接寫出![]() ,
,![]() ,
,![]() 的一個數量關系式.
的一個數量關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,![]() 、
、![]() 、
、![]() 在第二象限,橫坐標分別是-4、-2、-1,雙曲線
在第二象限,橫坐標分別是-4、-2、-1,雙曲線![]() 過
過![]() 、
、![]() 、
、![]() 三點,且
三點,且![]() .
.
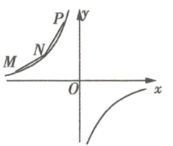
(1)求雙曲線的解析式;
(2)過![]() 點的直線
點的直線![]() 交
交![]() 軸于
軸于![]() ,交
,交![]() 軸于
軸于![]() ,且
,且![]() ,且交
,且交![]() 于另一點
于另一點![]() ,求
,求![]() 點坐標;
點坐標;
(3)以![]() 為邊(順時針方向)作正方形
為邊(順時針方向)作正方形![]() ,平移正方形使
,平移正方形使![]() 落在
落在![]() 軸上,點
軸上,點![]() 、
、![]() 對應的點
對應的點![]() 、
、![]() 正好落在反比例函數
正好落在反比例函數![]() 上,求
上,求![]() 對應點
對應點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某數學活動小組選定測量小河對岸大樹BC的高度,他們在斜坡上D處測得大樹頂端B的仰角是30°,朝大樹方向下坡走6米到達坡底A處,在A處測得大樹頂端B的仰角是45°,若坡角∠FAE=30°,求大樹的高度(結果保留根號).
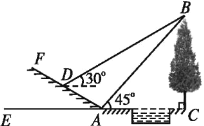
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,弦CD⊥AB于點H,過CD的延長線上一點E作⊙O的切線交AB的延長線于點F,切點為點G,連接AG交CD于點K.
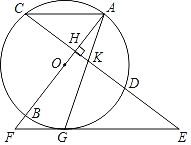
(1)求證:△EKG是等腰三角形;
(2)若KG2=KDGE,求證:AC∥EF;
(3)在(2)的條件下,若tanE=![]() ,AK=2
,AK=2![]() ,求FG的長.
,求FG的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com