
【題目】已知:正方形ABCD,等腰直角三角板的直角頂點落在正方形的頂點D處,使三角板繞點D旋轉.
(1)當三角板旋轉到圖1的位置時,猜想CE與AF的數量關系,并加以證明;
(2)在(1)的條件下,若DE:AE:CE= 1: ![]() :3,求∠AED的度數;
:3,求∠AED的度數;
(3)若BC= 4,點M是邊AB的中點,連結DM,DM與AC交于點O,當三角板的一邊DF與邊DM重合時(如圖2),若OF=![]() ,求CN的長.
,求CN的長.

【答案】(1)CE=AF;證明見解析;(2)135°;(3)![]() .
.
【解析】試題分析: (1)由正方形額等腰直角三角形的性質判斷出△ADF≌△CDE即可;
(2)設DE=k,表示出AE,CE,EF,判斷出△AEF為直角三角形,即可求出∠AED;
(3)由AB∥CD,得出![]() ,求出DM,DO,再判斷出△DFN∽△DCO,得到
,求出DM,DO,再判斷出△DFN∽△DCO,得到![]() ,求出DN即可.
,求出DN即可.
試題解析:
(1)CE=AF;
證明:在正方形ABCD,等腰直角三角形CEF中,
FD=DE,CD=CA,∠ADC=∠EDF=90°
∴∠ADF=∠CDE,
∴△ADF≌△CDE,
∴CE=AF,
(2)設DE=k,
∵DE:AE:CE=1: ![]() :3
:3
∴AE=![]() k,CE=AF=3k,
k,CE=AF=3k,
∴EF=![]() k,
k,
∵AE2+EF2=7k2+2k2=9k2,AF2=9k2,
即AE2+EF2=AF2
∴△AEF為直角三角形,
∴∠BEF=90°
∴∠AED=∠AEF+DEF=90°+45°=135°;
(3)∵M是AB中點,
∴MA=![]() AB=
AB=![]() AD,
AD,
∵AB∥CD,
∴![]() ,
,
在Rt△DAM中,DM=![]() ,
,
∴DO=![]() ,
,
∵OF=![]() ,
,
∴DF=![]() ,
,
∵∠DFN=∠DCO=45°,∠FDN=∠CDO,
∴△DFN∽△DCO,
∴![]() ,
,
∴ ,
,
∴DN=![]() ,
,
∴CN=CD-DN=4-![]() =
=![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD和過C點的切線互相垂直,垂足為D.
(1)求證:AC平分∠DAB;
(2)過點O作線段AC的垂線OE,垂足為E(要求:尺規作圖,保留作圖痕跡,不寫作法);
(3)若CD=4,AC=4![]() ,求垂線段OE的長.
,求垂線段OE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數y=mx2-(2m+1)x+m-5的圖象與x軸有兩個公共點.
(![]() )求m的取值范圍;
)求m的取值范圍;
(![]() )若m取滿足條件的最小的整數,
)若m取滿足條件的最小的整數,
①寫出這個二次函數的表達式;
②當n≤x≤1時,函數值y的取值范圍是-6≤y≤4-n,求n的值;
③將此二次函數圖象平移,使平移后的圖象經過原點O.設平移后的圖象對應的函數表達式為y=a(x-h)2 +k,當x<2時,y隨x的增大而減小,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】出租車司機小李某天下午運營全是在東西走向的人民大道上進行的,如果規定向東為正,向西為負,他這天下午行駛里程如下:(單位:千米)
+15, -3, +14,-11,+10,-12,+4,-15,+16,-18
(1)他將最后一名乘客送到目的地時,距下午出車地點是多少千米?
(2)若汽車耗油量為![]() 升∕千米,這天下午共耗油多少升
升∕千米,這天下午共耗油多少升
查看答案和解析>>
科目:初中數學 來源: 題型:
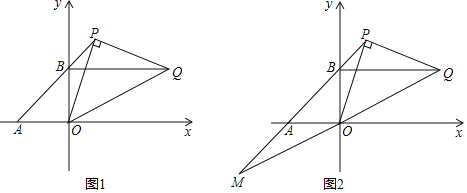
【題目】已知:如圖,直線AB交兩坐標軸于A(a,0)、B(0,b)兩點,且a,b滿足等式:![]() +(b﹣4)2=0,點P為直線AB上第一象限內的一動點,過P作OP的垂線且與過B點且平行于x軸的直線相交于點Q,
+(b﹣4)2=0,點P為直線AB上第一象限內的一動點,過P作OP的垂線且與過B點且平行于x軸的直線相交于點Q,
(1)求A,B兩點的坐標;
(2)當P點在直線AB上的第一象限內運動時,![]() AP﹣BQ的值變不變?如果不變,請求出這個定值;若變化請說明理由.
AP﹣BQ的值變不變?如果不變,請求出這個定值;若變化請說明理由.
(3)延長QO與直線AB交于點M.請判斷出線段AP,BM,PM三條線段構成三角形的形狀,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列調查方式,你認為最合適的是( )
A.為了了解同學們對央視《主持人大賽》欄目的喜愛程度,小華在學校隨機采訪了![]() 名七年級學生
名七年級學生
B.咸陽機場對旅客上飛機進行安檢,采用抽樣調查方式
C.為了了解西安市七年級學生的身高情況,采用全面調查方式
D.為了了解我省居民的日平均用電量,采用抽樣調查方式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABCD的邊長為1,點P為正方形內一動點,若點M在AB上,且滿足△PBC∽△PAM,延長BP交AD于點N,連結CM.

(1)如圖一,若點M在線段AB上,求證:AP⊥BN;AM=AN;
(2)①如圖二,在點P運動過程中,滿足△PBC∽△PAM的點M在AB的延長線上時,AP⊥BN和AM=AN是否成立?
②是否存在滿足條件的點P,使得PC=![]() ?(不需說明理由).
?(不需說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E是矩形ABCD的邊CD上一點,把△ADE沿AE對折,點D的對稱點F恰好落在BC上,已知折痕AE=![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么該矩形的周長為________.
,那么該矩形的周長為________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家買了一輛小轎車,小明連續記錄了一周每天行駛的路程:

請你用學過的統計知識解決下面的問題:
(1)小明家的轎車每月(按30天計算)要行駛多少千米?
(2)若每行駛100千米需汽油8升,汽油每升6.64元,請你算出小明家一年(按12個月計算)的汽油費用大約是多少元(精確到百位).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com