
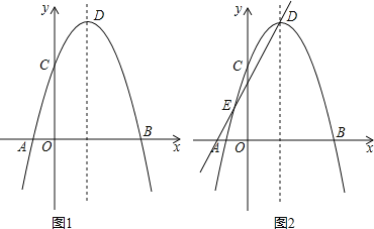
【題目】如圖1,在平面直角坐標系xOy中,拋物線y=-(x-a)(x-4)(a<0)與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,點D為拋物線的頂點.
(1)若D點坐標為(![]() ),求拋物線的解析式和點C的坐標;
),求拋物線的解析式和點C的坐標;
(2)若點M為拋物線對稱軸上一點,且點M的縱坐標為a,點N為拋物線在x軸上方一點,若以C、B、M、N為頂點的四邊形為平行四邊形時,求a的值;
(3)直線y=2x+b與(1)中的拋物線交于點D、E(如圖2),將(1)中的拋物線沿著該直線方向進行平移,平移后拋物線的頂點為D′,與直線的另一個交點為E′,與x軸的交點為B′,在平移的過程中,求D′E′的長度;當∠E′D′B′=90°時,求點B′的坐標.
【答案】(1)y=-x2+3x+4,C(0,4);(2)a1=-2-2![]() ,a2=
,a2=![]() ;(3)D′E′=2
;(3)D′E′=2![]() ,B′(-1,0).
,B′(-1,0).
【解析】
(1)將點D的坐標代入函數解析式,求得a的值;利用拋物線解析式來求點C的值.
(2)需要分類討論:BC為邊和BC為對角線兩種情況,根據“平行四邊形的對邊平行且相等,平行四邊形的對角線相互平分”的性質列出方程組,利用方程思想解答.
(3)根據平移規律得到D′E′的長度、平移后拋物線的解析式,然后由函數圖象上點的坐標特征求得點B′的坐標.
(1)依題意得:![]() =-(
=-(![]() -a)(
-a)(![]() -4).
-4).
解得a=-1.
∴拋物線解析式為:y=-(x+1)(x-4)或y=-x2+3x+4.
∴C(0,4).
(2)由題意知:A(a,0),B(4,0),C(0,-4a).
對稱軸為直線x=![]() ,則M(
,則M(![]() ,a).
,a).
①MN∥BC且MN=BC,根據點的平移特征可知N(![]() ,-3a).
,-3a).
則-3a=-(![]() -a)(
-a)(![]() -4).
-4).
解得:a=-2±2![]() (舍去正值).
(舍去正值).
②當BC為對角線時,設N(x,y).
根據平行四邊形的對角線互相平分可得: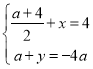 .
.
解得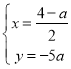 .
.
則-5a=-(![]() -a)(
-a)(![]() -4).
-4).
解得a=![]() .(舍去正值)
.(舍去正值)
∴a1=-2-2![]() ,a2=
,a2=![]() .
.
(3)把D(![]() )代入y=2x+b得到:2×
)代入y=2x+b得到:2×![]() +b=
+b=![]() .則b=
.則b=![]() .
.
故直線解析式為:y=2x+![]() .
.
聯立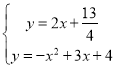 .
.
解得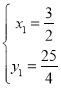 (舍去),
(舍去),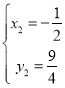 .
.
∴E(-![]() ,
,![]() )
)
∴DE=2![]() .
.
根據拋物線的平移規律,則平移后線段D′E′始終等于2![]() .
.
設平移后的D′(m,2m+![]() ),則E′(m-2,2m-
),則E′(m-2,2m-![]() ).
).
平移后拋物線的解析式為:y=-(x-m)2+2m+![]() .
.
則D′B′:y=-![]() x+n過點(m,2m+
x+n過點(m,2m+![]() ),
),
∴y=-![]() x+
x+![]() m+
m+![]() ,則B′(5m+
,則B′(5m+![]() ,0).
,0).
∴-![]() (5m+
(5m+![]() )+
)+![]() m+
m+![]() =0.
=0.
解得m1=-![]() ,m2=-
,m2=-![]() .
.
∴B′1(-1,0),B′2(-![]() ,0)(與D′重合,舍去).
,0)(與D′重合,舍去).
綜上所述,B′(-1,0).


 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案科目:初中數學 來源: 題型:
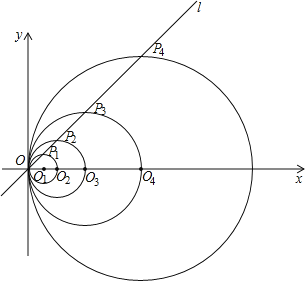
【題目】如圖,在平面直角坐標系中,直線l的函數表達式為y=x,點O1的坐標為(1,0),以O1為圓心,O1O為半徑畫圓,交直線l于點P1,交x軸正半軸于點O2,以O2為圓心,O2O為半徑畫圓,交直線l于點P2,交x軸正半軸于點O3,以O3為圓心,O3O為半徑畫圓,交直線l于點P3,交x軸正半軸于點O4;…按此做法進行下去,其中![]() 的長_____
的長_____
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解居民用水情況,小明在某小區隨機抽查了20戶家庭的月用水量,結果如下表:
月用水量(m3) | 4 | 5 | 6 | 8 | 9 |
戶數 | 4 | 5 | 7 | 3 | 1 |
則關于這20戶家庭的月用水量,下列說法錯誤的是( )
A.中位數是6m![]() B.平均數是5.8m
B.平均數是5.8m![]()
C.眾數是6m![]() D.極差是6m
D.極差是6m![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】可以用如下方法求方程x2-2x-2=0的實數根的范圍:利用函數y=x2-2x-2的圖象可知,當x=0時,y<0,當x=-1時,y>0,所以方程有一個根在-1和0之間.
(1)參考上面的方法,求方程x2-2x-2=0的另一個根在哪兩個連續整數之間;
(2)若方程x2-2x+c=0有一個根在0和1之間,求c的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年9月,我國中小學生迎來了新版“教育部統編義務教育語文教科書”,本次“統編本”教材最引人關注的變化之一是強調對傳統文化經典著作的閱讀,某校對A《三國演義》、B《紅樓夢》、C《西游記》、D《水滸》四大名著開展“最受歡迎的傳統文化經典著作”調查,隨機調查了若干名學生(每名學生必選且只能選這四大名著中的一部)并將得到的信息繪制了下面兩幅不完整的統計圖:

(1)本次一共調查了 名學生;
(2)請將條形統計圖補充完整;
(3)某班語文老師想從這四大名著中隨機選取兩部作為學生暑期必讀書籍,請用樹狀圖或列表的方法求恰好選中《三國演義》和《紅樓夢》的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,一張矩形紙片ABCD,其中AD=8cm,AB=6cm,先沿對角線BD折疊,點C落在點C′的位置,BC′交AD于點G.


(1)求證:BG=DG;
(2)求C′G的長;
(3)如圖2,再折疊一次,使點D與A重合,折痕EN交AD于M,求EM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮企業生產部有技術工人15人,生產部為了合理制定產品的每月生產定額,統計了這15人某月的加工零件個數:
每人加工零件個數 | 540 | 450 | 300 | 240 | 210 | 120 |
人數 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)寫出這15人該月加工零件數的平均數、中位數和眾數.
(2)假如生產部負責人把每位工人的月加工零件個數定為260,你認為這個定額是否合理?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,房間地面的圖案是用大小相同的黑、白正方形鑲嵌而成,圖中,第1個黑色L形由3個正方形組成,第2個黑色L形由7個正方形組成,…,那么組成第8個黑色L形的正方形個數為( )

A.31B.20C.37D.33
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com