
【題目】關于三角函數有如下的公式:
sin(α+β)=sinαcosβ+cosαsinβ①
cos(α+β)=cosαcosβ﹣sinαsinβ②
tan(α+β)=![]() ③
③
利用這些公式可將某些不是特殊角的三角函數轉化為特殊角的三角函數來求值,如:
tan105°=tan(45°+60°)=![]() =﹣(2+
=﹣(2+![]() ).
).
根據上面的知識,你可以選擇適當的公式解決下面的實際問題:
如圖,直升飛機在一建筑物CD上方A點處測得建筑物頂端D點的俯角α=60°,底端C點的俯角β=75°,此時直升飛機與建筑物CD的水平距離BC為42m,求建筑物CD的高.
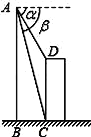
【答案】84米
【解析】分析:
如圖,過點D作DE⊥AB于點E,由題意易得∠ACB=75°,∠ABC=90°,DE=BC=42m,∠ADE=60°,這樣在Rt△ABC和在Rt△ADE中,結合題中所給關系式分別求出AB和AE的長,即可由CD=BE=AB-AE求得結果了.
詳解:
如圖,過點D作DE⊥AB于點E,由題意可得∠ACB=75°,∠ABC=90°,DE=BC=42m,CD=BE,∠ADE=60°,
∴在Rt△ABC和Rt△ADE
AB=BCtan75°=42tan75°=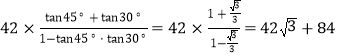 ,
,
AE=![]() ,
,
∴CD=AB﹣AE=![]() (米).
(米).
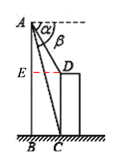
答:建筑物CD的高為84米.
睛:讀懂題意,把已知量和未知量轉化到Rt△ABC和Rt△ADE中,這樣利用直角三角形中邊角間的關系結合題目中所給的“兩角和的三角形函數公式”即可使問題得到解決.


科目:初中數學 來源: 題型:
【題目】定義:若a+b=2,則稱a與b是關于1的平衡數.
(1)①3與 是關于1的平衡數;②4﹣x與 是關于1的平衡數(用含x的代數式表示).
(2)若a=2x2﹣3(x2+x)﹣4,b=2x﹣[3x﹣(4x+x2)﹣2],判斷a與b是否是關于1的平衡數,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】日歷上的規律:表格是2020年元月的日歷,圖中的陰影區域是在日歷中選取的一塊九宮格.
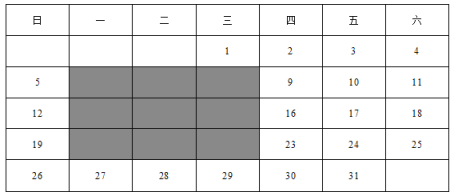
(1)九宮格中,四個角的四個數之和與九宮格中央那個數有什么關系?
(2)請你自選一塊九宮格進行計算,看四個角上的四個數之和與九宮格中央那個數是否還有這種關系?
(3)試說明原理.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】童星玩具廠工人的工作時間為:每月22天,每天8小時.工資待遇為:按件計酬,多勞多得,每月另加福利工資500元,按月結算.該廠生產A、B兩種產品,工人每生產一件A種產品可得報酬1.50元,每生產一件B種產品可得報酬2.80元.該廠工人可以選擇A、B兩種產品中的一種或兩種進行生產.工人小李生產1件A產品和1件B產品需35分鐘;生產3件A產品和2件B產品需85分鐘.
(1)小李生產1件A產品需要 分鐘,生產1件B產品需要 分鐘.
(2)求小李每月的工資收入范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下列等式:
![]() ,
,
將以上二個等式兩邊分別相加得:
![]()
用你發現的規律解答下列總是:
(1)直接寫出下列各式的計算結果:
①![]() _______________________
_______________________
②![]() ______________________
______________________
(2)仿照題中的計算形式,猜想并寫出:![]() ___________________________
___________________________
(3)解方程:![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形網格中的每個小正方形的邊長都是1,每個小格的頂點叫做格點.
(1)在圖1中以格點為頂點畫一個面積為10的正方形;
(2)在圖2中以格點為頂點畫一個三角形,使三角形三邊長分別為2、![]() 、
、![]() ;
;
(3)如圖3,點A、B、C是小正方形的頂點,求∠ABC的度數.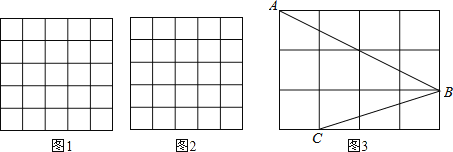
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知平而直角坐標系xOy(如圖),二次函數y=ax2+bx+4的圖像經過A(-2,0)、
B(4,0)兩點,與y軸交于點C點.
(1)求這個二次函數的解析式;
(2)如果點E在線段OC上,且∠CBE=∠ACO,求點E的坐標;
(3)點M在y軸上,且位于點C上方,點N在直線BC上,點P為上述二次函數圖像的對稱軸上的點,如果以C、M、N、P為頂點的四邊形是菱形,求點M的坐標.
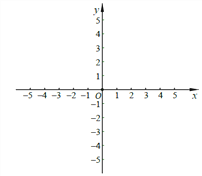
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某出租車駕駛員從公司出發,在南北向的人民路上連續接送5批客人,行駛路程記錄如下(規定向南為正,向北為負,單位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
|
|
|
|
|
(1)接送完第5批客人時,該駕駛員在公司什么方向,距離公司多遠?
(2)若該出租車的收費標準為:行駛路程不超過![]() ,收費10元;超過
,收費10元;超過![]() ,對超過部分另加收每千米1.8元.當送完第5批客人時,該駕駛員共收到車費多少元?
,對超過部分另加收每千米1.8元.當送完第5批客人時,該駕駛員共收到車費多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com